【题目】如图,在平面直角坐标系中,正方形OABC的边长为4,顶点A,C分别在x轴、y轴的正半轴上,抛物线y=-![]() x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
x2+bx+c经过点B,C两点,点D为抛物线的顶点,连接AC,BD,CD.
(1)求此抛物线的解析式;
(2)求此抛物线顶点D的坐标和四边形ABDC的面积.

参考答案:
【答案】 (1) y=-![]() x2+2x+4;(2)顶点D(2,6),S四边形ABDC=12.
x2+2x+4;(2)顶点D(2,6),S四边形ABDC=12.
【解析】试题分析:(1)根据题意确定出B与C的坐标,代入抛物线解析式求出b与c的值,即可确定出解析式;
(2)把抛物线解析式化为顶点形式,找出顶点坐标,四边形ABDC面积=三角形ABC面积+三角形BCD面积,求出即可.
试题解析:(1)由已知得:C(0,4),B(4,4),
把B与C坐标代入y=-![]() x2+bx+c得:
x2+bx+c得: ![]() ,
,
解得:b=2,c=4,
则解析式为y=-![]() x2+2x+4;
x2+2x+4;
(2)∵y=-![]() x2+2x+4=-
x2+2x+4=-![]() (x-2)2+6,
(x-2)2+6,
∴抛物线顶点坐标为(2,6),
则S四边形ABDC=S△ABC+S△BCD=![]() ×4×4+
×4×4+![]() ×4×2=8+4=12.
×4×2=8+4=12.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了方便行人,市政府打算修建如图所示的过街天桥,桥面AD平行于地面BC,立柱AE⊥BC于点E,立柱DF⊥BC于点F,若AB=5
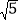 米,tanB=
米,tanB= ,∠C=30°.
,∠C=30°.(1)求桥面AD与地面BC之间的距离.
(2)因受地形限制,决定对该天桥进行改建,使CD斜面的坡度变陡,将其30°坡角改为40°,改建后斜面为DG,试计算此次改建节省路面宽度CG大约应是多少?(结果精确到0.1米,参考数据:sin40°≈0.64,cos40°≈0.77,tan40°≈0.84,
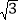 ≈1.732)
≈1.732)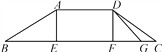
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系
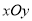 中,
中,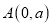 ,
,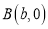 分别在
分别在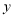 轴正半轴和
轴正半轴和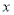 轴负半轴上,
轴负半轴上,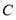 在第二象限,满足:
在第二象限,满足: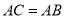 ,
,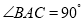 .已知
.已知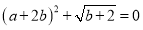 .
.(1)求
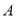 ,
,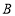 的坐标;
的坐标;(2)求点
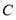 的坐标及
的坐标及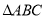 的面积;
的面积;(3)已知
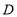 是
是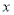 轴的正半轴上一点,
轴的正半轴上一点,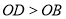 ,
,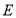 在第一象限,
在第一象限,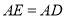 ,
,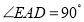 ,连接
,连接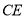 交
交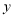 轴于点
轴于点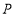 .
.①求证:
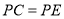 .
.②在点
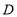 的移动过程中,给出以下两个结论:(i)
的移动过程中,给出以下两个结论:(i)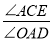 的值不变;(ii)
的值不变;(ii)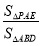 的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值.
的值不变,其中有且只有一个是正确的,请你找出这个结论并求其值. 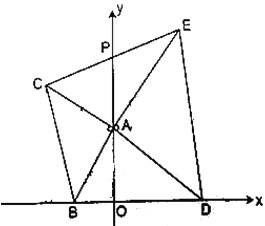
-
科目: 来源: 题型:
查看答案和解析>>【题目】我国中东部地区雾霾天气趋于严重,环境治理已刻不容缓.我市某电器商场根据民众健康需要,代理销售某种家用空气净化器,其进价是200元/台.经过市场销售后发现:在一个月内,当售价是400元/台时,可售出200台,且售价每降低10元,就可多售出50台.若供货商规定这种空气净化器售价不能低于300元/台,代理销售商每月要完成不低于450台的销售任务.
(1)试确定月销售量y(台)与售价x(元/台)之间的函数关系式;
(2)求售价x的范围;
(3)当售价x(元/台)定为多少时,商场每月销售这种空气净化器所获得的利润w(元)最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】有这样一个问题:探究函数y=-
 +|x|的图象与性质.
+|x|的图象与性质.
小军根据学习函数的经验,对函数y=- +|x|的图象与性质进行了探究.
+|x|的图象与性质进行了探究.
下面是小军的探究过程,请补充完整:
(1)函数y=- +|x|的自变量x的取值范围是 ;
+|x|的自变量x的取值范围是 ;
(2)表是y与x的几组对应值.x
-2
-1.9
-1.5
-1
-0.5
0
1
2
3
4
…
y
2
1.60
0.80
0
-0.72
-1.41
-0.37
0
0.76
1.55
…
在平面直角坐标系xOy中,描出了以上表中各对对应值为坐标的点,根据描出的点,画出该函数的图象;

(3)观察图象,函数的最小值是 ;
(4)进一步探究,结合函数的图象,写出该函数的一条性质(函数最小值除外): . -
科目: 来源: 题型:
查看答案和解析>>【题目】某校组织部分学参加安全知识竞赛,并将成绩整理后绘制成直方图,图中从左至右前四组的百分比分别是4%,12%,40%,28%,第五组的频数是8.则:①参加本次竞赛的学生共有100人;②第五组的百分比为16%;③成绩在70-80分的人数最多;④80分以上的学生有14名;其中正确的个数有( )
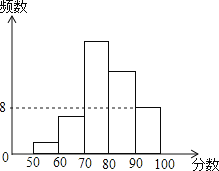
A.1个B.2个C.3个D.4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:
 .
.(2)解不等式
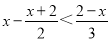 ,并把解集在数轴上表示出来.
,并把解集在数轴上表示出来.
(3)解方程组:
 .
.
相关试题

