【题目】如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
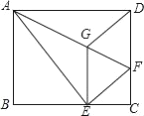
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=![]() GF×AF;
GF×AF;
(3)若![]() ,折痕AF=5
,折痕AF=5![]() cm,则矩形ABCD的周长为 .
cm,则矩形ABCD的周长为 .
参考答案:
【答案】(1)证明见解析;(2)证明见解析;(3)36cm.
【解析】试题分析:(1)先依据翻折的性质和平行线的性质证明∠DGF=∠DFG,从而得到GD=DF,接下来依据翻折的性质可证明DG=GE=DF=EF。
(2)连接DE,交AF于点O.由菱形的性质可知GF⊥DE,OG=OF=![]() GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
GF,接下来,证明△DOF∽△ADF,由相似三角形的性质可证明DF2=FOAF,于是可得到GE、AF、FG的数量关系.
(3)过点G作GH⊥DC,垂足为H.利用(2)的结论可求得FG=4,然后再△ADF中依据勾股定理可求得AD的长,然后再证明△FGH∽△FAD,利用相似三角形的性质可求得GH的长,最后依据BE=AD-GH求解即可.
试题解析:
(1)证明:如图所示,
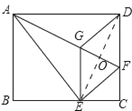
∵EG∥CD, ∴∠EGF=∠DFG.
∵由折叠的性质可知:GD=GE,DF=EF,∠DGF=∠EGF,
∴∠DGF=∠DFG. ∴GD=DF.
∴GD=GE=DF=EF,∴四边形EFDG为菱形;
(2)证明:如图所示,连接DE,交AF于点O.
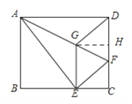
∵四边形EFDG为菱形, ∴GF⊥DE,OG=OF=![]() GF.
GF.
∵∠DOF=∠ADF=90°,∠OFD=∠DFA, ∴△DOF∽△ADF.
∴![]() ,即DF2=OFAF.
,即DF2=OFAF.
∵OF=![]() GF,DF=EG, ∴EG2=
GF,DF=EG, ∴EG2=![]() GFAF ;
GFAF ;
(3)矩形ABCD的周长为36 cm.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧
 分别交OA、OB于点M、N.
分别交OA、OB于点M、N.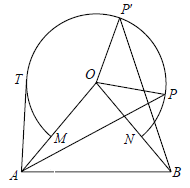
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′. 求证:AP = BP′;
(2)点T在左半弧上,若AT与弧
 相切于点T,求点T到OA的距离;
相切于点T,求点T到OA的距离;(3)设点Q在优弧
 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数. -
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校“阅读工程”的开展情况.市教育局从该校初中生中随机抽取了150名学生进行了阅读情况的问卷调查,绘制了如下不完全的统计图:
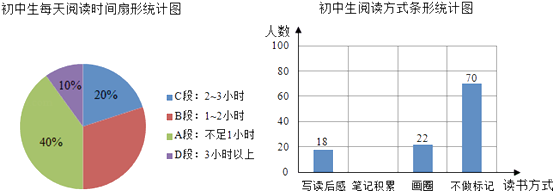
根据上述统计图提供的信息,解答下列问题:
(1)每天阅读时间在1﹣2小时学生有多少人?
(2)采用“笔记积累”阅读方式的学生有多少人?
(3)补全条形统计图.
(4)若将写读后感、笔记积累、画圈点读三种方式称为记忆阅读,求笔记积累人数占有记忆阅读人数的百分比. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(x﹣5)2+7的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】m为何值时,关于x的方程2x-3m=x的解是4x-2m=3x-1的解的2倍?
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列各组代数式中,没有公因式的是( )
A. ax+y和x+y B. 2x和4y C. a-b和b-a D. -x2+xy和y-x
-
科目: 来源: 题型:
查看答案和解析>>【题目】学生的学业负担过重会严重影响学生对待学习的态度.为此我市教育部门对部分学校的八年级学生对待学习的态度进行了一次抽样调查(把学习态度分为三个层级,A级:对学习很感兴趣;B级:对学习较感兴趣;C级:对学习不感兴趣),并将调查结果绘制成图①和图②的统计图(不完整).请根据图中提供的信息,解答下列问题:
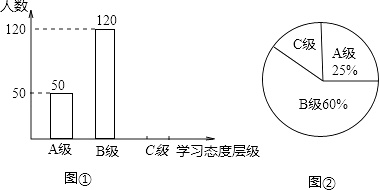
(1)此次抽样调查中,共调查了名学生;
(2)将图①补充完整;
(3)求出图②中C级所占的圆心角的度数;
(4)根据抽样调查结果,请你估计我市近8000名八年级学生中大约有多少名学生学习态度达标(达标包括A级和B级)?
相关试题

