【题目】如图所示,△OAB中,OA=OB=10,∠AOB=80°,以点O为圆心,6为半径的优弧![]() 分别交OA、OB于点M、N.
分别交OA、OB于点M、N.
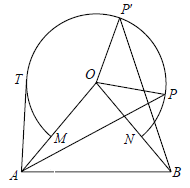
(1)点P在右半弧上(∠BOP是锐角),将OP绕点O逆时针旋转80°得OP′. 求证:AP = BP′;
(2)点T在左半弧上,若AT与弧![]() 相切于点T,求点T到OA的距离;
相切于点T,求点T到OA的距离;
(3)设点Q在优弧![]() 上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
上,当△AOQ的面积最大时,直接写出∠BOQ的度数.
参考答案:
【答案】(1)根据已知得出∠AOP=∠BOP′,从进而由SAS得出△AOP≌△BOP′,即可得出答案。
(2)![]()
(3)10°或170°
【解析】试题分析:(1)首先根据已知得出∠AOP=∠BOP′,进而得出△AOP≌△BOP′,即可得出答案;
(2)利用切线的性质得出∠ATO=90°,再利用勾股定理求出AT的长,进而得出TH的长即可得出答案;
(3)当OQ⊥OA时,△AOQ面积最大,且左右两半弧上各存在一点分别求出即可.
试题解析:(1)如图1,

∵∠AOP=∠AOB+∠BOP=80°+∠BOP,
∠BOP′=∠POP′+∠BOP=80°+∠BOP,
∴∠AOP=∠BOP′,
∵在△AOP和△BOP′中

∴△AOP≌△BOP′(SAS),
∴AP=BP′;
(2)如图1,连接OT,过点T作TH⊥OA于点H,
∵AT与弧MN相切,
∴∠ATO=90°,
∴AT=![]() =
=![]() =8,
=8,
∵![]() ×OA×TH=
×OA×TH=![]() ×AT×OT,
×AT×OT,
即![]() ×10×TH=
×10×TH=![]() ×8×6,
×8×6,
解得:TH=![]() ,即点T到OA的距离为
,即点T到OA的距离为![]() ;
;
(3)如图2,当OQ⊥OA时,△AOQ的面积最大;

理由:∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ+∠AOB=90°+80°=170°,
当Q点在优弧MN右侧上,
∵OQ⊥OA,
∴QO是△AOQ中最长的高,则△AOQ的面积最大,
∴∠BOQ=∠AOQ-∠AOB=90°-80°=10°,
综上所述:当∠BOQ的度数为10°或170°时,△AOQ的面积最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知|﹣x+1|+(y+2)2=0,则x+y=( )
A. ﹣3 B. ﹣1 C. 3 D. 1
-
科目: 来源: 题型:
查看答案和解析>>【题目】如果2a-3b=-3,那么代数式5-2a+3b的值是 ( ).
A. 0 B. 2 C. 5 D. 8
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法:①两点之间的所有连线中,线段最短;②相等的角是对顶角; ③过一点有且仅有一条直线与己知直线垂直; ④两点之间的距离是两点间的线段;⑤若AB=BC,则点B为线段AC的中点。其中正确的个数是( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了解某校“阅读工程”的开展情况.市教育局从该校初中生中随机抽取了150名学生进行了阅读情况的问卷调查,绘制了如下不完全的统计图:
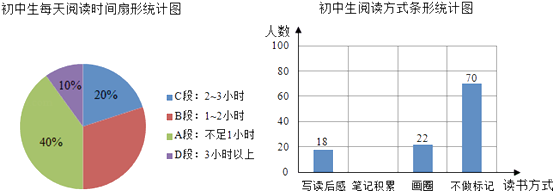
根据上述统计图提供的信息,解答下列问题:
(1)每天阅读时间在1﹣2小时学生有多少人?
(2)采用“笔记积累”阅读方式的学生有多少人?
(3)补全条形统计图.
(4)若将写读后感、笔记积累、画圈点读三种方式称为记忆阅读,求笔记积累人数占有记忆阅读人数的百分比. -
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=(x﹣5)2+7的最小值是_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将矩形ABCD沿AF折叠,使点D落在BC边的点E处,过点E作EG∥CD交AF于点G,连接DG.
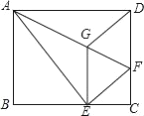
(1)求证:四边形EFDG是菱形;
(2)求证:EG2=
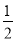 GF×AF;
GF×AF;(3)若
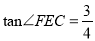 ,折痕AF=5
,折痕AF=5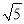 cm,则矩形ABCD的周长为 .
cm,则矩形ABCD的周长为 .
相关试题

