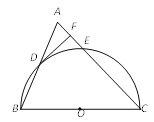
【题目】(9分)如图,△ABC为等腰三角形,AC=BC,以边BC为直径的半圆与边AB,AC分别交于D,E两点,过点D作DF⊥AC,垂足为点F.
(1)判断DF与⊙O的位置关系,并证明你的结论;
(2)若BC=9,EF=1,求DF的长.
参考答案:
【答案】(1)DF与⊙O相切.证明见解析;(2)2![]() .
.
【解析】试题分析:(1)、连接OD,根据已知条件得出OD∥AC,从而得出切线;(2)、过点O作OG⊥EC,得出四边形OGFD为矩形,然后根据勾股定理求出OG的长度.
试题解析:(1)DF与⊙O相切.
连接OD. ∵AC=BC,OB=OD, ∴∠B=∠A ∠B=∠1 ∴∠A=∠1 ∴OD∥AC.
∵DF⊥AC ∴∠AFD=90° ∴∠ODF=∠AFD=90°
又∵OD是⊙O的半径 ∴DF与⊙O相切.
(2)过O作OG⊥EC交EC于点G.∵∠ODF=∠AFD=90° ∴四边形OGFD是矩形.
∴DF=OG,FG=OD=![]() BC=
BC=![]() ∵OG⊥EC, ∴CG=EG=FG-EF=
∵OG⊥EC, ∴CG=EG=FG-EF=![]() -1=
-1=![]() .
.
∴DF=OG=![]() =
=![]() =2
=2![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校九年级有15名同学参加校运会百米比赛,预赛成绩各不相同,前7名才有资格参加决赛,小明已经知道了自己的成绩,但他想知道自己能否进入决赛,还需要知道这15名同学成绩的_____.(填“极差”、“众数”或“中位数”)
-
科目: 来源: 题型:
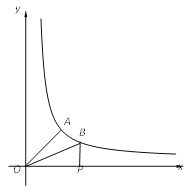
查看答案和解析>>【题目】如图,已知A、B是反比例函数y=
 图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP=
图象上两点,BP⊥x轴,垂足为P.已知∠AOP=45°,OA=4, tan∠BOP= .
.(1)求点A的坐标;
(2)连接AB,求四边形AOPB的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一组数据共有50个,分成5组后其中前四组的频数分别是3、17、15、5, 则第5组数据的频率为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若(a2+b2)(a2+b2+3)=10,则a2+b2=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,D是BC边的中点,DE⊥AB,DF⊥AC,垂足分别为E,F,且DE=DF,求证:

(1)BE=CF;
(2)AB=AC. -
科目: 来源: 题型:
查看答案和解析>>【题目】港珠澳大桥总长度5500000米被称为“新世界七大奇迹之一”,则数字5500000用科学记数法表示为( )
A.55×105B.55×106C.0.55×105D.5.5×105
相关试题

