【题目】如图①,△ABC中,AB=AC,点M、N分别是AB、AC上的点,且AM=AN.连接MN、CM、BN,点D、E、F、G分别是BC、MN、BN、CM的中点,连接E、F、D、G.
(l)判断四边形EFDG的形状是 (不必证明);
(2)现将△AMN绕点A旋转一定的角度,其他条件不变(如图②),四边形EFDG的形状是否发生变化?证明你的结论;
(3)如图②,在(2)的情况下,请将△ABC在原有的条件下添加一个条件,使四边形EFDG是正方形.请写出你添加的条件,并在添加条件的基础上证明四边形EFDG是正方形.

参考答案:
【答案】(1)菱形;(2)不变,证明见解析;(3)添加条件:∠BAC=90°,证明见解析.
【解析】
(1) 四边形EFDG是平行四边形, 理由为: 如图1,连接AM,由E、F,G、H分别为中点,利用利用中位线定理得到两组对边相等, 即可得证;
(2) 如图②, 由旋转得∠BAM=∠CAN, △BAM≌△CAN(SAS), BM=CN,点E、F分别是MN、BN的中点,可得EF∥DG,EF=DG,可得四边形EFDG是平行四边形,可得FD=![]() BM=EF,所以四边形EFDG是菱形;
BM=EF,所以四边形EFDG是菱形;
(3) 设BM与CN交于点P,DF与BM交于点Q,由∠ABM=∠CAN,∠ABC+∠ACB=90°可得∠BPC=90°,∠BQD=90°,∠FDG=90°,所以菱形EFDG是正方形.
解:(1)四边形EFDG是菱形,
∵点D、E、F、G分别是BC、MN、BN、CM的中点,
∴EF是△NBM的中位线,DG是△CBM的中位线,EG是△CMN的中位线,DF是△BCN的中位线,
∴EF=DG=![]() BM,EG=DF=
BM,EG=DF=![]() CN,
CN,
∵AB=AC,AM=AN,
∴BM=CN,
∴EF=DF=EG=DG,
∴四边形EFDG是菱形,
故答案为:菱形;
(2)不变,
证明:由旋转得∠BAM=∠CAN,
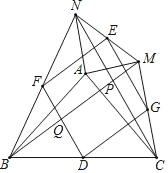
在△BAM和△CAN中,
∵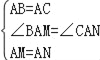 ,
,
∴△BAM≌△CAN(SAS),
∴BM=CN,
∵点E、F分别是MN、BN的中点,
∴EF∥BM,EF=![]() BM,
BM,
同理,DG∥BM,DG=![]() BM,FD=
BM,FD=![]() CN,
CN,
∴EF∥DG,EF=DG,
∴四边形EFDG是平行四边形,
∴EF∥CN,BM=CN,
∴FD=![]() BM=EF,
BM=EF,
∴四边形EFDG是菱形;
(3)添加条件:∠BAC=90°,
证明:如图,设BM与CN交于点P,DF与BM交于点Q,
由(2)得∠ABM=∠ACN,
∵∠BAC=90°,
∴∠ABC+∠ACB=90°,
∴(∠ABC﹣∠ABM)+(∠ACB+∠ACN)=90°,即∠PBC+∠PCB=90°,
∴∠BPC=90°,
∵DF∥CN,
∴∠BQD=90°,
∵DG∥BM,
∴∠FDG=90°,
∴菱形EFDG是正方形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:请你添加一个条件_____可以得到
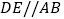
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,是一块破损的木板.
(1)请你设计一种方案,检验木板的两条直线边缘 AB、CD 是否平行;
(2)若 AB∥CD,连接 BC,过点 A 作 AM⊥BC 于 M,垂足为 M,画出图形,并写出∠BCD 与∠BAM 的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:抛物线y=
 (x﹣1)2﹣3.
(x﹣1)2﹣3.
(1)写出抛物线的开口方向、对称轴;
(2)函数y有最大值还是最小值?并求出这个最大(小)值;
(3)设抛物线与y轴的交点为P,与x轴的交点为Q,求直线PQ的函数解析式. -
科目: 来源: 题型:
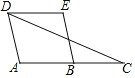
查看答案和解析>>【题目】如图,∵DE∥BC(已知),∴∠1=____(____),∠2=_______(_____)又∵∠1=∠2(已知),∴∠B=∠C(____),∵∠3=∠B(已知),∴∠3=∠C(_________),∴DF∥AC(______)

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在四边形ABCD中,E、F分别是CD、AB延长线上的点,连结EF,分别交AD、BC于点G、H.若∠1=∠2,∠A=∠C,试说明AD//BC和AB//CD.请完成下面的推理过程,填写理由或数学式:

∵∠1=∠2,∠1=∠AGH(_________)
∴∠2=∠AGH(________)
∴AD//BC(________)
∴∠ADE=∠C(________)
∵∠A=∠C(已知)
∴∠ADE=_______(等量代换)
∴AB//CD(_______)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程变形正确的是( )
A. 方程3x-2=2x+1移项,得3x-2x=-1+2
B. 方程3-x=2-5(x-1)去括号,得3-x=2-5x-1
C. 方程
 =1可化为3x=6
=1可化为3x=6D. 方程
 x=-
x=- 系数化为1,得x=-1
系数化为1,得x=-1
相关试题

