搜索
【题目】下列方程变形正确的是( )
A. 方程3x－2＝2x＋1移项，得3x－2x＝－1＋2
B. 方程3－x＝2－5(x－1)去括号，得3－x＝2－5x－1
C. 方程
＝1可化为3x＝6
D. 方程
x＝－
系数化为1，得x＝－1
参考答案：
【答案】C
【解析】
方程得变形一般包括去分母，去括号，移项，合并同类项，系数化为1，结合这些方法对每一个选项的方程进行变形，进而做出判断.
A项，对方程3x－2＝2x＋1，移项，得3x－2x＝2＋1，所以A项变形错误；B项，对方程3－x＝2－5(x－1)，去括号，得3－x＝2－5x＋5，所以B项错误；C项，对于方程
－
＝1，化简，得3x＝6，所以C项正确；D项，对于方程
x＝－
，系数化为1，得x＝－
，所以D项错误.答案选C.
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，△ABC中，AB=AC，点M、N分别是AB、AC上的点，且AM=AN．连接MN、CM、BN，点D、E、F、G分别是BC、MN、BN、CM的中点，连接E、F、D、G．
（l）判断四边形EFDG的形状是 （不必证明）；
（2）现将△AMN绕点A旋转一定的角度，其他条件不变（如图②），四边形EFDG的形状是否发生变化？证明你的结论；
（3）如图②，在（2）的情况下，请将△ABC在原有的条件下添加一个条件，使四边形EFDG是正方形．请写出你添加的条件，并在添加条件的基础上证明四边形EFDG是正方形．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，∵DE∥BC（已知），∴∠1=____（____），∠2=_______（_____）又∵∠1=∠2（已知），∴∠B=∠C（____），∵∠3=∠B（已知），∴∠3=∠C（_________），∴DF∥AC（______）
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在四边形ABCD中，E、F分别是CD、AB延长线上的点，连结EF，分别交AD、BC于点G、H．若∠1=∠2，∠A=∠C，试说明AD//BC和AB//CD．请完成下面的推理过程，填写理由或数学式:
∵∠1=∠2，∠1=∠AGH（_________）
∴∠2=∠AGH（________）
∴AD//BC（________）
∴∠ADE=∠C（________）
∵∠A=∠C（已知）
∴∠ADE=_______（等量代换）
∴AB//CD（_______）
-
科目： 来源： 题型：
查看答案和解析>>【题目】在日历上，我们可以发现其中某些数满足一定的规律，如图是2017年12月份的日历．如图所选择的两组四个数，分别将每组数中相对的两数相乘，再相减，例如：7×9﹣1×15= ，18×20﹣12×26= ，不难发现，结果都是 ．
（1）请将上面三个空补充完整；
（2）我们发现选择其他类似的部分规律也相同，请你利用整式的运算对以上的规律加以证明．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB是⊙O的直径，AC是弦．
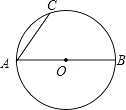
（1）请你按下面步骤画图（画图或作辅助线时先使用铅笔画出，确定后必须使用黑色字迹的签字笔描黑）； 第一步，过点A作∠BAC的角平分线，交⊙O于点D；
第二步，过点D作AC的垂线，交AC的延长线于点E．
第三步，连接BD．
（2）求证：AD2=AEAB；
（3）连接EO，交AD于点F，若5AC=3AB，求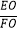
的值． -
科目： 来源： 题型：
查看答案和解析>>【题目】某学校在商场购买甲、乙两种不同足球，购买甲种足球共花费2000元，购买乙种足球共花费1400元，购买甲种足球数量是购买乙种足球数量的2倍，且购买一个乙种足球比购买一个甲种足球多花20元．
（1）求购买一个甲种足球、一个乙种足球各需多少元？
（2）为响应“足球进校园”的号召，这所学校决定再次购买甲、乙两种足球共50个．恰逢该商场对两种足球的售价进行调整，甲种足球售价比第一次购买时提高了10%，乙种足球售价比第一次购买时降低了10%，如果此次购买甲、乙两种足球的总费用不超过2900元，那么这所学校最多可购买多少个乙种足球？
相关试题
