【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD. 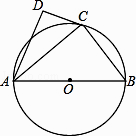
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线.
参考答案:
【答案】
(1)解:∵AB是⊙O直径,C在⊙O上,
∴∠ACB=90°,
又∵BC=3,AB=5,
∴由勾股定理得AC=4
(2)证明:连接OC
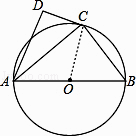
∵AC是∠DAB的角平分线,
∴∠DAC=∠BAC,
又∵AD⊥DC,
∴∠ADC=∠ACB=90°,
∴△ADC∽△ACB,
∴∠DCA=∠CBA,
又∵OA=OC,
∴∠OAC=∠OCA,
∵∠OAC+∠OBC=90°,
∴∠OCA+∠ACD=∠OCD=90°,
∴DC是⊙O的切线.
【解析】(1)首先根据直径所对的圆周角为直角得到直角三角形,然后利用勾股定理求得AC的长即可;(2)连接OC,证OC⊥CD即可;利用角平分线的性质和等边对等角,可证得∠OCA=∠CAD,即可得到OC∥AD,由于AD⊥CD,那么OC⊥CD,由此得证.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某电器商销售一种微波炉和电磁炉,微波炉每台定价
 元,电磁炉每台定价
元,电磁炉每台定价 元.“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.
元.“双十一”期间商场决定开展促销活动,活动期间向客户提供两种优惠方案.方案一:买一台微波炉送一台电磁炉;
方案二:微波炉和电磁炉都按定价的
 付款.
付款.现某客户要到该卖场购买微波炉
 台,电磁炉
台,电磁炉 台
台 .
. 若该客户按方案一购买,需付款________元.(用含
若该客户按方案一购买,需付款________元.(用含 的代数式表示)若该客户按方案二购买,需付款________元.(用含
的代数式表示)若该客户按方案二购买,需付款________元.(用含 的代数式表示)
的代数式表示) 若
若 时,通过计算说明此时按哪种方案购买较为合算?
时,通过计算说明此时按哪种方案购买较为合算? 当
当 时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法.
时,你能给出一种更为省钱的购买方案吗?试写出你的购买方法. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,反比例函数y=
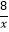 的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0). 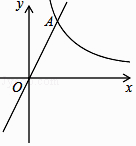
(1)求平移后直线的表达式;
(2)求OA平移后所得直线与双曲线的交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一组相同规格的饭碗,测得一只碗高度为4.5cm,两只饭碗整齐叠放在桌面上的高度为6.5cm,三只饭碗整齐叠放在桌面上的高度为8.5cm.根据以上信息回答下列问题:
(1)若饭碗数为
 个,用含
个,用含 的代数式表示
的代数式表示 个饭碗整齐叠放在桌面上的高度;
个饭碗整齐叠放在桌面上的高度;(2)当叠放饭碗数为9个时,求这叠饭碗的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线L:y=ax2+bx+c与已知抛物线y=
 x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)
x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)
(1)求L的解析式;
(2)若L与x轴的交点为A,B(A在B的左侧),与y轴的交点为C,求△ABC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差
(单位:千克)



1
2
箱数
2
6
10
8
4
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
相关试题

