【题目】抛物线L:y=ax2+bx+c与已知抛物线y= ![]() x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)
x2的图像的形状相同,开口方向也相同,且顶点坐标为(﹣2,﹣4)
(1)求L的解析式;
(2)若L与x轴的交点为A,B(A在B的左侧),与y轴的交点为C,求△ABC的面积.
参考答案:
【答案】
(1)解:∵y=ax2+bx+c与已知抛物线y= ![]() x2的图像的形状相同,开口方向也相同,
x2的图像的形状相同,开口方向也相同,
∴a= ![]() ,
,
∵抛物线的顶点坐标为(﹣2,﹣4),
∴y= ![]() (x+2)2﹣4;
(x+2)2﹣4;
(2)解:∵L与x轴的交点为A,B(A在B的左侧),与y轴的交点为C, ∴y=0,则0= ![]() (x+2)2-4, 解得:x1=-6,x2=2, 当x=0时,y=-3, 故A(-6,0),B(2,0),C(0,-3),
(x+2)2-4, 解得:x1=-6,x2=2, 当x=0时,y=-3, 故A(-6,0),B(2,0),C(0,-3),
则△ABC的面积为: ![]() ×AB×CO=
×AB×CO= ![]() ×8×3=12.
×8×3=12.
【解析】(1)直接利用二次函数的性质得出a的值,进而利用顶点式求出答案;(2)首先求出二次函数与坐标轴的交点,进而得出AB,CO的长,即可得出答案.
【考点精析】认真审题,首先需要了解抛物线与坐标轴的交点(一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.),还要掌握相似三角形的性质(对应角相等,对应边成比例的两个三角形叫做相似三角形)的相关知识才是答题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在平面直角坐标系xOy中,反比例函数y=
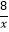 的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0).
的图像与正比例函数y=kx(k≠0)的图像相交于横坐标为2的点A,平移直线OA,使它经过点B(3,0). 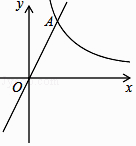
(1)求平移后直线的表达式;
(2)求OA平移后所得直线与双曲线的交点坐标. -
科目: 来源: 题型:
查看答案和解析>>【题目】有一组相同规格的饭碗,测得一只碗高度为4.5cm,两只饭碗整齐叠放在桌面上的高度为6.5cm,三只饭碗整齐叠放在桌面上的高度为8.5cm.根据以上信息回答下列问题:
(1)若饭碗数为
 个,用含
个,用含 的代数式表示
的代数式表示 个饭碗整齐叠放在桌面上的高度;
个饭碗整齐叠放在桌面上的高度;(2)当叠放饭碗数为9个时,求这叠饭碗的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,⊙O的直径为AB,点C在圆周上(异于A,B),AD⊥CD.
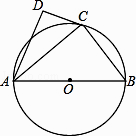
(1)若BC=3,AB=5,求AC的值;
(2)若AC是∠DAB的平分线,求证:直线CD是⊙O的切线. -
科目: 来源: 题型:
查看答案和解析>>【题目】(3分)如图,AD是△ABC的角平分线,DE⊥AC,垂足为E,BF∥AC交ED的延长线于点F,若BC恰好平分∠ABF,AE=2BF.给出下列四个结论:①DE=DF;②DB=DC;③AD⊥BC;④AC=3BF,其中正确的结论共有( )

A. 4个 B. 3个 C. 2个 D. 1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】有30箱苹果,以每箱20千克为标准,超过或不足的千克数分别用正、负数来表示,记录如下:
与标准质质量的差
(单位:千克)



1
2
箱数
2
6
10
8
4
(1)这30箱苹果中,最重的一箱比最轻的一箱重多少千克?
(2)与标准质量比较,这30箱苹果总计超过或不足多少千克?
(3)若苹果每千克售价6元,则出售这30箱苹果可卖多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是两块完全一样的含30°角的直角三角尺,分别记做△ABC与△A′B′C′,现将两块三角尺重叠在一起,设较长直角边的中点为M,绕中点M转动上面的三角尺ABC,使其直角顶点C恰好落在三角尺A′B′C′的斜边A′B′上.当∠A=30°,AC=10时,两直角顶点C,C′间的距离是_____.

相关试题

