搜索
【题目】计算
（1）计算：π0+2﹣1﹣ 
﹣|﹣ 
|；
（2）
，其中x=4，y=﹣2．
参考答案：
【答案】
（1）解：原式=1+ 
﹣ ﹣ 
=1﹣
= 
；
（2）解：原式= 
，
当x=4，y=﹣2时，
原式= 
．
【解析】（1）分别根据0指数幂、负整数指数幂及绝对值的性质计算出各数，再根据有理数混合运算的法则进行计算即可；（2）先根据分式混合运算的法则把原式进行化简，再把x=4，y=﹣2代入进行计算即可．
【考点精析】掌握零指数幂法则和整数指数幂的运算性质是解答本题的根本，需要知道零次幂和负整数指数幂的意义： a0=1（a≠0）;a-p=1/ap（a≠0，p为正整数）；aman=am+n(m、n是正整数)；（am）n=amn(m、n是正整数)；(ab)n=anbn(n是正整数)；am/an=am-n(a不等于0，m、n为正整数）；（a/b）n=an/bn(n为正整数)．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=2，AC=BC=
．
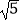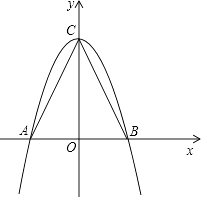
（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；
（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4﹣4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2﹣4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，∴y1=1，y2=﹣1．
当x2=3，即y2=3，∴y3=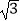
，y4=﹣ ．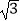
所以，原方程的解是y1=1，y2=﹣1，y3=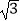 ，y4=﹣ ．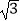
再如x2﹣2=4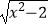
，可设y= 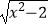，用同样的方法也可求解． -
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数按要求分类．
﹣2，5，
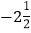，0，﹣3.4，﹣21，π，
，3.7，15%；正数集合：{_____…}，
负整数集合：{_____…}，
分数集合：{_____…}
非正数集合：{_____…}
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，已知∠A=80°，∠B=60°，DE∥BC，那么∠CED的大小是（ ）
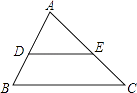
A.40°
B.60°
C.120°
D.140° -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）2﹣（﹣7）﹣13+（﹣7）
（2）18﹣6÷（﹣2）×（﹣
）（3）﹣23÷[（﹣2）3﹣（﹣4）]
（4）（0.25﹣
﹣
）×（﹣36）（5）0﹣23÷（﹣4）3﹣
（6）﹣32×（﹣2）+42÷（﹣2）3﹣|﹣22|；
-
科目： 来源： 题型：
查看答案和解析>>【题目】求代数式的值．
（1）（6a2﹣2ab）﹣2（3a2+4ab﹣
b2）其中a＝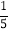
，b＝﹣1．（2）已知A＝a2﹣2ab+b2，B＝a2+2ab+b2
①求2A﹣B；
②如果2A﹣3B+C＝0，那么C的表达式是什么？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，△ABC是边长为6的等边三角形，P是AC边上一动点，由A向C运动(与A、C不重合)，Q是CB延长线上一点，与点P同时以相同的速度由B向CB延长线方向运动(Q不与B重合)，过P作PE⊥AB于E，连接PQ交AB于D.
(1)当∠BQD=30°时，求AP的长；
(2)证明：在运动过程中，点D是线段PQ的中点；
(3)当运动过程中线段ED的长是否发生变化？如果不变，求出线段ED的长；如果变化请说明理由.
相关试题
