搜索
【题目】如图，在△ABC中，已知∠A=80°，∠B=60°，DE∥BC，那么∠CED的大小是（ ）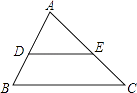 
A.40°
B.60°
C.120°
D.140°
参考答案：
【答案】D
【解析】解：∵∠A+∠B+∠C=180°， ∴∠C=180°﹣∠A﹣∠B=180°﹣80°﹣60°=40°，
又∵DE∥BC，
∴∠CED+∠C=180°，
∴∠CED=180°﹣40°=140°．
故选D．
【考点精析】本题主要考查了平行线的性质和三角形的内角和外角的相关知识点，需要掌握两直线平行，同位角相等；两直线平行，内错角相等；两直线平行，同旁内角互补；三角形的三个内角中，只可能有一个内角是直角或钝角；直角三角形的两个锐角互余；三角形的一个外角等于和它不相邻的两个内角的和；三角形的一个外角大于任何一个和它不相邻的内角才能正确解答此题．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某大酒店有108个相同规格的房间需要装饰．一天，3名师傅去装饰8个房间，结果其中有40平方米未来得及装饰；同样一天5名徒弟去恰好装饰完9个房间．已知每名师傅比徒弟一天多装饰30平方米．
(1)求每个房间需要装饰的面积；
(2)每名师傅每天装饰多少平方米？每名徒弟呢？
(3)若由1名师傅带2名徒弟去装饰这108个房间，需要几天才能完成？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，AB=2，AC=BC=
．
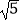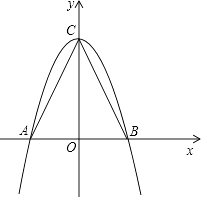
（1）以AB所在的直线为x轴，AB的垂直平分线为y轴，建立直角坐标系如图，请你分别写出A、B、C三点的坐标；
（2）求过A、B、C三点且以C为顶点的抛物线的解析式；
（3）若D为抛物线上的一动点，当D点坐标为何值时，S△ABD=
S△ABC；
（4）如果将（2）中的抛物线向右平移，且与x轴交于点A′B′，与y轴交于点C′，当平移多少个单位时，点C′同时在以A′B′为直径的圆上（解答过程如果有需要时，请参看阅读材料）．
附：阅读材料
一元二次方程常用的解法有配方法、公式法和因式分解法，对于一些特殊方程可以通过换元法转化为一元二次方程求解．如解方程：y4﹣4y2+3=0．
解：令y2=x（x≥0），则原方程变为x2﹣4x+3=0，解得x1=1，x2=3．
当x1=1时，即y2=1，∴y1=1，y2=﹣1．
当x2=3，即y2=3，∴y3=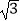
，y4=﹣ ．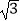
所以，原方程的解是y1=1，y2=﹣1，y3=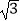 ，y4=﹣ ．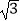
再如x2﹣2=4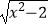
，可设y= 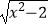，用同样的方法也可求解． -
科目： 来源： 题型：
查看答案和解析>>【题目】把下列各数按要求分类．
﹣2，5，
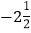，0，﹣3.4，﹣21，π，
，3.7，15%；正数集合：{_____…}，
负整数集合：{_____…}，
分数集合：{_____…}
非正数集合：{_____…}
-
科目： 来源： 题型：
查看答案和解析>>【题目】计算
（1）计算：π0+2﹣1﹣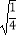
﹣|﹣ 
|；
（2）
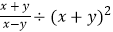，其中x=4，y=﹣2． -
科目： 来源： 题型：
查看答案和解析>>【题目】计算：
（1）2﹣（﹣7）﹣13+（﹣7）
（2）18﹣6÷（﹣2）×（﹣
）（3）﹣23÷[（﹣2）3﹣（﹣4）]
（4）（0.25﹣
﹣
）×（﹣36）（5）0﹣23÷（﹣4）3﹣
（6）﹣32×（﹣2）+42÷（﹣2）3﹣|﹣22|；
-
科目： 来源： 题型：
查看答案和解析>>【题目】求代数式的值．
（1）（6a2﹣2ab）﹣2（3a2+4ab﹣
b2）其中a＝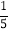
，b＝﹣1．（2）已知A＝a2﹣2ab+b2，B＝a2+2ab+b2
①求2A﹣B；
②如果2A﹣3B+C＝0，那么C的表达式是什么？
相关试题
