【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为![]() ,依次类推,排在第
,依次类推,排在第![]() 位的数称为第
位的数称为第![]() 项,记为
项,记为![]() .
.
一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母![]() 表示(
表示(![]() ).如:数列1,3,9,27,…为等比数列,其中
).如:数列1,3,9,27,…为等比数列,其中![]() ,公比为
,公比为![]() .
.
则:(1)等比数列3,6,12,…的公比![]() 为_____________,第4项是________________.
为_____________,第4项是________________.
(2)如果一个数列![]() ,
, ![]() ,
, ![]() ,
, ![]() ,…是等比数列,且公比为
,…是等比数列,且公比为![]() ,那么根据定义可得到:
,那么根据定义可得到:
![]() ,
, ![]() ,
, ![]() ,……
,…… ![]() .
.
∴![]() ,
, ![]() ,
, ![]() ,
, ![]()
由此可得:an=____________________(用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
参考答案:
【答案】 2 an=a1qn-1 5, 40
【解析】试题分析:(1)根据等比数列的定义可得;
(2)由数列中的每一项等于首项乘以公比的序数减一次方可得;
(3)根据定义先求得首项,再根据通项公式即可得.
试题解析::(1)根据题意知公比q=6÷3=2,第4项是12×2=24;
(2)根据定义我们可依次写出这个数列的每一项:a1,a1q,a1q2,a1q3,….由此可得第n项an=a1qn-1;
(3)根据题意知,第1项为10÷2=5,第4项为5×23=40.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
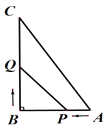
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )

A.3cmB.6cmC.12cmD.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD,BE⊥CD,AD=3,DE=4,则BE= ______ .

-
科目: 来源: 题型:
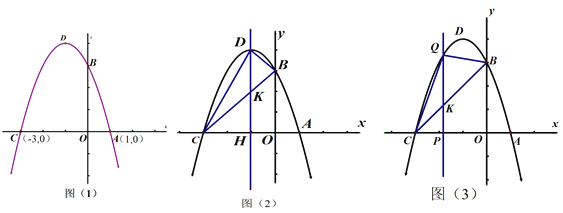
查看答案和解析>>【题目】已知,如图,抛物线与x轴交点坐标为A(1,0),C(-3,0),
(1)若已知顶点坐标D为(-1,4)或B点(0,3),选择适当方式求抛物线的解析式.
(2)若直线DH为抛物线的对称轴,在(1)的基础上,求线段DK的长度,并求△DBC的面积.
(3)将图(2)中的对称轴向左移动,交x轴于点p(m,0)(-3<m<-1),与线段BC、抛物线的交点分别为点K、Q,用含m的代数式表示QK的长度,并求出当m为何值时,△BCQ的面积最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系xOy中,抛物线
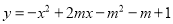 交 y轴于点为A,顶点为D,对称轴与x轴交于点H.
交 y轴于点为A,顶点为D,对称轴与x轴交于点H.(1)求顶点D的坐标(用含m的代数式表示);
(2)当抛物线过点(1,-2),且不经过第一象限时,平移此抛物线到抛物线
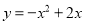 的位置,求平移的方向和距离;
的位置,求平移的方向和距离;(3)当抛物线顶点D在第二象限时,如果∠ADH=∠AHO,求m的值.
相关试题

