【题目】已知:如图所示,在△ABC中,∠B=90°,AB=5cm,BC=7cm,点P从点A开始沿AB边向点B以1cm/s的速度移动,点Q从点B开始沿BC边向点C以2cm/s的速度移动.
(1)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ的面积等于4cm2?
(2)如果P,Q分别从A,B同时出发,那么几秒后,△PBQ中PQ的长度等于5cm?
(3)在(1)中,当P,Q出发几秒时,△PBQ有最大面积?
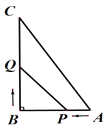
参考答案:
【答案】(1)1秒后,△PBQ的面积等于4cm2;(2)2秒后,△PBQ中PQ的长度等于5cm;(3)当t=2.5时,面积最大.
【解析】试题分析:(1)经过x秒钟,△PBQ的面积等于4cm2,根据点P从A点开始沿AB边向点B以1cm/s的速度移动,点Q从B点开始沿BC边向点C以2cm/s的速度移动,表示出BP和BQ的长可列方程求解;
(2)利用勾股定理列出方程求解即可;
(3)根据题意列出△PBQ的面积与x的函数关系式即可解决.
试题解析:(1)设t秒后,△PBQ的面积等于4cm2,
则列方程为:(5-t)×2t×![]() =4,
=4,
解得t1=1,t2=4(舍),
答:1秒后,△PBQ的面积等于4cm2.
(2)设x秒后,△PBQ中PQ的长度等于5cm,
列方程为:(5-x)2+(2x)2=52,
解得x1=0(舍),x2=2,
答:2秒后,△PBQ中PQ的长度等于5cm。
(3)设面积为Scm2,时间为t,
则S=(5-t)×2t×![]() =-t2+5t,
=-t2+5t,
当t=2.5时,面积最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】能用平方差公式计算的是( )
A.(-x+2y)(x-2y)B.(2x-y)(2y+x)C.(m-n)(n-m)D.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点O在边AB上,以点O为圆心,OA为半径的圆经过点C,过点C作直线MN,使∠BCM=2∠A.
(1)判断直线MN与⊙O的位置关系,并说明理由;
(2)若OA=4,∠BCM=60°,求图中阴影部分的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在下列条件中:①∠A+∠B=∠C,②∠A:∠B:∠C=1: 2:3,③∠A=90°﹣∠B,④∠A=∠B=∠C中,能确定△ABC是直角三角形的条件有( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,点P关于OA、OB的对称点分别是P1,P2,线段P1P2分别交OA、OB于D、C,P1P2=6cm,则△PCD的周长为( )

A.3cmB.6cmC.12cmD.无法确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读理解题:
按照一定顺序排列着的一列数称为数列,排在第一位的数称为第1项,记为
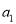 ,依次类推,排在第
,依次类推,排在第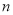 位的数称为第
位的数称为第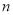 项,记为
项,记为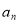 .
.一般地,如果一个数列从第二项起,每一项与它前一项的比等于同一个常数,那么这个数列叫做等比数列,这个常数叫做等比数列的公比,公比通常用字母
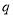 表示(
表示(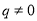 ).如:数列1,3,9,27,…为等比数列,其中
).如:数列1,3,9,27,…为等比数列,其中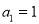 ,公比为
,公比为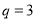 .
.则:(1)等比数列3,6,12,…的公比
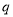 为_____________,第4项是________________.
为_____________,第4项是________________.(2)如果一个数列
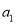 ,
, 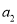 ,
, 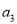 ,
, 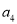 ,…是等比数列,且公比为
,…是等比数列,且公比为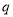 ,那么根据定义可得到:
,那么根据定义可得到: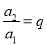 ,
, 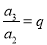 ,
, 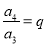 ,……
,…… 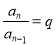 .
.∴
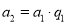 ,
,  ,
, 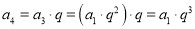 ,
, 
由此可得:an=____________________(用a1和q的代数式表示)
(3)若一等比数列的公比q=2,第2项是10,请求它的第1项与第4项.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,∠ACB=90°,AC=BC,AD⊥CD,BE⊥CD,AD=3,DE=4,则BE= ______ .

相关试题

