【题目】对于一元二次方程![]() (
(![]() ,
,![]() ,
,![]() ,
,![]() 为常数),下列说法:
为常数),下列说法:
①方程的解为![]() ;
;
②若![]() ,则方程必有一根为
,则方程必有一根为![]() ;
;
③若![]() ,则一元二次方程
,则一元二次方程![]() 必有一根为
必有一根为![]() ;
;
④若![]() ,则方程
,则方程![]() 有两个不等实数根;
有两个不等实数根;
⑤若![]() ,则方程
,则方程![]() 有两个相等的实数根,
有两个相等的实数根,
正确的结论是________.
参考答案:
【答案】②③④
【解析】
有当△=b2-4ac>0时,方程的解为![]() ,由此即可判定说法错误;
,由此即可判定说法错误;
②首先把b=a+c变为a-b+c=0,当x=-1时,ax2+bx+c=a-b+c,由此即可判定说法正确;
③首先把b=2a+![]() c变为4a-2b+c=0,当x=-2时,ax2+bx+c=4a-2b+c,由此即可判定说法正确;
c变为4a-2b+c=0,当x=-2时,ax2+bx+c=4a-2b+c,由此即可判定说法正确;
④首先由ac<0,可得方程cx2+bx+a=0是一元二次方程,再根据△=b2-4ac>0,可得方程cx2+bx+a=0有两个不等实数根,由此即可判定说法正确;
⑤只有当c≠0时,方程cx2+bx+a=0是一元二次方程,若b2-4ac=0,则方程cx2+bx+a=0有两个相等的实数根,由此即可判定说法错误.
①对于一元二次方程ax2+bx+c=0(a≠0,a,b,c为常数),
当△=b2-4ac<0时,方程无解;
当△=b2-4ac≥0时,方程的解为![]() ,故原说法错误;
,故原说法错误;
②∵b=a+c,
∴a-b+c=0,
∴当x=-1时,ax2+bx+c=a-b+c=0,
∴x=-1为方程ax2+bx+c=0的一根,故原说法正确;
③∵b=2a+![]() c,
c,
∴4a-2b+c=0,
∴当x=-2时,ax2+bx+c=4a-2b+c=0,
∴一元二次方程ax2+bx+c=0必有一根为x=-2,故原说法正确;
④∵ac<0,
∴c≠0,方程cx2+bx+a=0是一元二次方程,
∵△=b2-4ac>0,
∴方程cx2+bx+a=0有两个不等实数根,故原说法正确;
⑤当c≠0时,方程cx2+bx+a=0是一元二次方程,若b2-4ac=0,则方程cx2+bx+a=0有两个相等的实数根;
当c=0时,b=0,方程cx2+bx+a=0不可能有两个相等的实数根,故原说法错误.
故答案是:②③④.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,点
中,点 、
、 分别在边
分别在边 、
、 上,如果
上,如果 ,且
,且 ,那么下列说法中,错误的是( )
,那么下列说法中,错误的是( )
A. △ADE∽△ABC B. △ADE∽△ACD
C. △ADE∽△DCB D. △DEC∽△CDB
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平面直角坐标系中,直线AB:
 交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.

-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道:选用同一长度单位量得两条线段
 、
、 的长度分别是
的长度分别是 ,
, ,那么就说两条线段的比
,那么就说两条线段的比 :
: ,如果把
,如果把 表示成比值
表示成比值 ,那么
,那么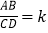 ,或
,或 .请完成以下问题:
.请完成以下问题: 四条线段
四条线段 ,
, ,
, ,
, 中,如果________,那么这四条线段
中,如果________,那么这四条线段 ,
, ,
, ,
, 叫做成比例线段.
叫做成比例线段. 已知
已知 ,那么
,那么 ________,
________, ________
________ 如果
如果 ,那么
,那么 成立吗?请用两种方法说明其中的理由.
成立吗?请用两种方法说明其中的理由. 如果
如果 ,求
,求 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
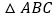 中,
中,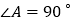 ,
,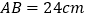 ,
,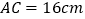 ,现有动点
,现有动点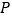 从点
从点 出发,沿射线
出发,沿射线 方向运动,动点
方向运动,动点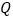 从点
从点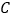 出发,沿射线
出发,沿射线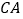 方向运动,已知点
方向运动,已知点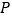 的速度是
的速度是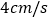 ,点
,点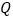 的速度是
的速度是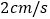 ,它们同时出发,经过________秒,
,它们同时出发,经过________秒,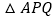 的面积是
的面积是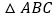 面积的一半?
面积的一半?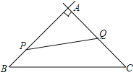
-
科目: 来源: 题型:
查看答案和解析>>【题目】某装备企业采用订单式生产销售某种产品,保证其销售量与产量相等,图中的线段
 ,线段
,线段 分别表示该产品每万台生产成本
分别表示该产品每万台生产成本 (单位:万元)、销售价
(单位:万元)、销售价 (单位:万元)与产量
(单位:万元)与产量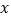 (单位:台)之间的函数关系,考虑企业的经济效益,当此种产品市场预定生产为
(单位:台)之间的函数关系,考虑企业的经济效益,当此种产品市场预定生产为 万台时,将停止订单生产销售,求当该产品产量为多少万台时,可实现
万台时,将停止订单生产销售,求当该产品产量为多少万台时,可实现 万元利润?
万元利润?
-
科目: 来源: 题型:
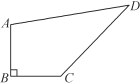
查看答案和解析>>【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=3
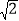 ,CD=8,AD=10.
,CD=8,AD=10.(1)求∠BCD的度数;
(2)求四边形ABCD的面积.
相关试题

