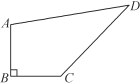
【题目】如图,在四边形ABCD中,∠B=90°,AB=BC=3![]() ,CD=8,AD=10.
,CD=8,AD=10.
(1)求∠BCD的度数;
(2)求四边形ABCD的面积.
参考答案:
【答案】(1)∠BCD=135°;(2) S四边形ABCD=33.
【解析】
(1)连接AC,在直角三角形ABC中,利用勾股定理求出AC的长,再由CD与AD的长,利用勾股定理的逆定理判断得到三角形ACD为直角三角形,再由等腰直角三角形的性质,根据∠BCD=∠ACB+∠ACD即可求出;
(2)四边形ABCD面积=三角形ABC面积+三角形ACD面积,求出即可.
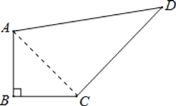
(1)连接AC, 在Rt△ABC中,∠B=90°,AB=BC=3![]() ,
,
根据勾股定理,得AC=![]() =6,∠ACB=45°,
=6,∠ACB=45°,
∵CD=8,AD=10,
∴![]() =
=![]() +
+![]() ,
,
∴△ACD为直角三角形,即∠ACD=90°,
则∠BCD=∠ACB+∠ACD=135°;
(2)根据题意,得S四边形ABCD=S△ABC+S△ACD
=![]() ×3
×3![]() ×3
×3![]() +
+![]() ×6×8
×6×8
=9+24
=33.
故答案为(1)∠BCD=135°;(2) S四边形ABCD=33.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校举办“迎省运”学生书画展览,现要在长方形展厅中划出
 个形状、大小完全一样的小长方形(中阴影部分)区城摆放展览作品.
个形状、大小完全一样的小长方形(中阴影部分)区城摆放展览作品.(1)如图1,若大长方形的长和宽分別为
 米和
米和 米,求小长方形的长和宽;
米,求小长方形的长和宽;
(2)如图2,若大长方形的长和宽分别为
 和
和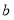 ,求出一个小长方形与一个大长方形周长的比值.
,求出一个小长方形与一个大长方形周长的比值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】有理数x,y在数轴上对应点如图所示:

(1)在数轴上表示﹣x,|y|;
(2)试把x,y,0,﹣x,|y|这五个数从小到大用“<”号连接,
(3)化简:|x+y|﹣|y﹣x|+|y|.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠B=90°,点E是AC的中点,AC=2AB,∠BAC的平分线AD交BC于点D,作AF∥BC,连接DE并延长交AF于点F,连接FC.
求证:四边形ADCF是菱形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了在即将到来的体育中考中取得好的成绩,某校准备在体育中考前将学校九年级的
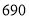 名学生送到体育馆进行一次模拟考试,经学校和客车公司联系了解到,
名学生送到体育馆进行一次模拟考试,经学校和客车公司联系了解到,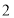 辆大型客车和
辆大型客车和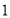 辆中型客车可载客
辆中型客车可载客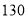 人,
人,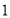 辆大型客车和
辆大型客车和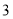 辆中型客车可载客
辆中型客车可载客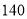 人,若要将这些学生--次性全部送到体育馆,且恰好装满.根据以上信息,回答下面问题:
人,若要将这些学生--次性全部送到体育馆,且恰好装满.根据以上信息,回答下面问题:(1)每辆大型客车和中型客车各载多少人?
(2)该校共有多少种租车方案?.
(3)若每辆大型客车需租金
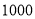 元,每辆中型客车需租金
元,每辆中型客车需租金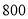 元,请你给该校提供一个最省钱的租车建议,并求出最少租车费用是多少?
元,请你给该校提供一个最省钱的租车建议,并求出最少租车费用是多少? -
科目: 来源: 题型:
查看答案和解析>>【题目】已知如图,在数轴上有A,B两点,所表示的数分别为
 ,
, ,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:
,点A以每秒5个单位长度的速度向右运动,同时点B以每秒3个单位长度的速度也向右运动,如果设运动时间为t秒,解答下列问题:
 运动前线段AB的长为______;运动1秒后线段AB的长为______;
运动前线段AB的长为______;运动1秒后线段AB的长为______; 运动t秒后,点A,点B运动的距离分别为______和______;
运动t秒后,点A,点B运动的距离分别为______和______; 求t为何值时,点A与点B恰好重合;
求t为何值时,点A与点B恰好重合; 在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由.
在上述运动的过程中,是否存在某一时刻t,使得线段AB的长为5,若存在,求t的值;若不存在,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】写出下列命题的逆命题,并判断这对命题的真假.
(1)三边对应相等的两个三角形全等;
(2)若a=b,则a2=b2;
(3)若∠α+∠β=180°,则∠α与∠β至少有一个是钝角.
相关试题

