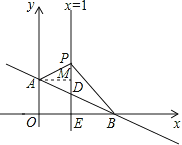
【题目】如图,平面直角坐标系中,直线AB:![]() 交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
交y轴于点A(0,1),交x轴于点B.直线x=1交AB于点D,交x轴于点E,P是直线x=1上一动点,且在点D的上方,设P(1,n).
(1)求直线AB的解析式和点B的坐标;
(2)求△ABP的面积(用含n的代数式表示);
(3)当S△ABP=2时,以PB为边在第一象限作等腰直角三角形BPC,求出点C的坐标.

参考答案:
【答案】(1) AB的解析式是y=-![]() x+1.点B(3,0).(2)
x+1.点B(3,0).(2)![]() n-1;(3) (3,4)或(5,2)或(3,2).
n-1;(3) (3,4)或(5,2)或(3,2).
【解析】
试题(1)把A的坐标代入直线AB的解析式,即可求得b的值,然后在解析式中,令y=0,求得x的值,即可求得B的坐标;
(2)过点A作AM⊥PD,垂足为M,求得AM的长,即可求得△BPD和△PAB的面积,二者的和即可求得;
(3)当S△ABP=2时,![]() n-1=2,解得n=2,则∠OBP=45°,然后分A、B、P分别是直角顶点求解.
n-1=2,解得n=2,则∠OBP=45°,然后分A、B、P分别是直角顶点求解.
试题解析:(1)∵y=-![]() x+b经过A(0,1),
x+b经过A(0,1),
∴b=1,
∴直线AB的解析式是y=-![]() x+1.
x+1.
当y=0时,0=-![]() x+1,解得x=3,
x+1,解得x=3,
∴点B(3,0).
(2)过点A作AM⊥PD,垂足为M,则有AM=1,
∵x=1时,y=-![]() x+1=
x+1=![]() ,P在点D的上方,
,P在点D的上方,
∴PD=n-![]() ,S△APD=
,S△APD=![]() PDAM=
PDAM=![]() ×1×(n-
×1×(n-![]() )=
)=![]() n-
n-![]()
由点B(3,0),可知点B到直线x=1的距离为2,即△BDP的边PD上的高长为2,
∴S△BPD=![]() PD×2=n-
PD×2=n-![]() ,
,
∴S△PAB=S△APD+S△BPD=![]() n-
n-![]() +n-
+n-![]() =
=![]() n-1;
n-1;
(3)当S△ABP=2时,![]() n-1=2,解得n=2,
n-1=2,解得n=2,
∴点P(1,2).
∵E(1,0),
∴PE=BE=2,
∴∠EPB=∠EBP=45°.
第1种情况,如图1,∠CPB=90°,BP=PC,过点C作CN⊥直线x=1于点N.
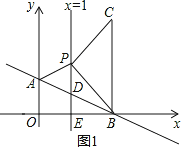
∵∠CPB=90°,∠EPB=45°,
∴∠NPC=∠EPB=45°.
又∵∠CNP=∠PEB=90°,BP=PC,
∴△CNP≌△BEP,
∴PN=NC=EB=PE=2,
∴NE=NP+PE=2+2=4,
∴C(3,4).
第2种情况,如图2∠PBC=90°,BP=BC,
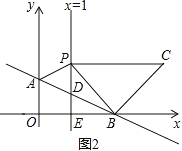
过点C作CF⊥x轴于点F.
∵∠PBC=90°,∠EBP=45°,
∴∠CBF=∠PBE=45°.
又∵∠CFB=∠PEB=90°,BC=BP,
∴△CBF≌△PBE.
∴BF=CF=PE=EB=2,
∴OF=OB+BF=3+2=5,
∴C(5,2).
第3种情况,如图3,∠PCB=90°,CP=EB,
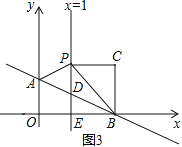
∴∠CPB=∠EBP=45°,
在△PCB和△PEB中,
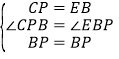
∴△PCB≌△PEB(SAS),
∴PC=CB=PE=EB=2,
∴C(3,2).
∴以PB为边在第一象限作等腰直角三角形BPC,点C的坐标是(3,4)或(5,2)或(3,2).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某县为了落实中央的“强基惠民工程”,计划将某村的居民自来水管道进行改造.该工程若由甲队单独施工恰好在规定时间内完成;若乙队单独施工,则完成工程所需天数是规定天数的1.5倍.如果由甲、乙队先合做15天,那么余下的工程由甲队单独完成还需5天.
(1)这项工程的规定时间是多少天?
(2)已知甲队每天的施工费用为6500元,乙队每天的施工费用为3500元.为了缩短工期以减少对居民用水的影响,工程指挥部最终决定该工程由甲、乙队合做来完成.则该工程施工费用是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)问题发现
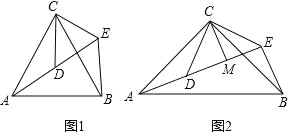
如图1,△ACB和△DCE均为等边三角形,点A,D,E在同一直线上,连接BE.填空:
①∠AEB的度数为______;
②线段AD,BE之间的数量关系为______.
(2)拓展探究
如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A,D,E在同一直线上,CM为△DCE中DE边上的高,连接BE,请判断∠AEB的度数及线段CM,AE,BE之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】寿县教育部门计划在3月12日植树节当天安排
 ,
, 两校部分学生到森林公园参加植树活动.已知
两校部分学生到森林公园参加植树活动.已知 校区的每位学生往返车费是6元,
校区的每位学生往返车费是6元, 校每位学生的往返车费是10元,要求两所学校均要有学生参加,且
校每位学生的往返车费是10元,要求两所学校均要有学生参加,且 校参加活动的学生比
校参加活动的学生比 校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求
校参加活动的学生少4人,本次活动的往返车费总和不超过210元.求 ,
, 两校最多各有多少学生参加?
两校最多各有多少学生参加? -
科目: 来源: 题型:
查看答案和解析>>【题目】图1是一个长为2m、宽为2n的长方形,沿图中虚线用剪刀均分成四块小长方形,然后按图2的形状拼成一个正方形.

(1)请用两种不同的方法求图2中阴影部分的面积.
方法1: ;
方法2: ;
(2)观察图2请你写出下列三个代数式:(m+n)2,(m-n)2,mn之间的等量关系 ;
(3)根据(2)题中的等量关系,解决如下问题:
①已知:
 ,
, ,求:
,求: 的值;
的值;②已知:
 ,
, ,求:
,求: 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如果一个正整数能表示成两个连续偶数的平方差,那么这个正整数为“神秘数”.
如:


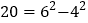
因此,4,12,20这三个数都是神秘数.
(1)28和2012这两个数是不是神秘数?为什么?
(2)设两个连续偶数为
 和
和 (其中
(其中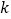 为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由.
为非负整数),由这两个连续偶数构造的神秘数是4的倍数,请说明理由. (3)两个连续奇数的平方差(取正数)是不是神秘数?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在一个不透明的袋子中装有仅颜色不同的10个小球,其中红球4个,黑球6个.
(1)先从袋子中取出m(m>1)个红球,再从袋子中随机摸出1个球,将“摸出黑球”记为事件A,请完成下列表格:事件A
必然事件
随机事件
m的值
(2)先从袋子中取出m个红球,再放入m个一样的黑球并摇匀,随机摸出1个黑球的概率等于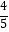 ,求m的值.
,求m的值.
相关试题

