【题目】星光橱具店购进电饭煲和电压锅两种电器进行销售,其进价与售价如表:
售价(元/台) | 售价(元/台) | |
电饭煲 | 200 | 250 |
电压锅 | 160 | 200 |
(1)一季度,橱具店购进这两种电器共30台,用去了5600元,并且全部售完,问橱具店在该买卖中赚了多少钱?
(2)为了满足市场需求,二季度橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个,且电饭煲的数量不少于23个,问橱具店有哪几种进货方案?并说明理由;
参考答案:
【答案】(1)赚了1400元;(2)有三种方案:①电饭煲23台,电压锅27台;②电饭煲24台,电压锅26台;③电饭煲25台,电压锅25台,
【解析】
()1)设橱具店购进电饭煲![]() 台,电压锅
台,电压锅![]() 台,根据橱具店购进这两种电器共30台且用去了5600元,即可得出关于
台,根据橱具店购进这两种电器共30台且用去了5600元,即可得出关于![]() 、
、![]() 的二元一次方程组,解之即可得出
的二元一次方程组,解之即可得出![]() 、
、![]() 的值,再根据总利润
的值,再根据总利润![]() 单个利润
单个利润![]() 购进数量即可得出结论;
购进数量即可得出结论;
(2)设购买电饭煲![]() 台,则购买电压锅
台,则购买电压锅![]() 台,根据橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个且电饭煲的数量不少于23个,即可得出关于
台,根据橱具店决定用不超过9000元的资金采购电饭煲和电压锅共50个且电饭煲的数量不少于23个,即可得出关于![]() 的一元一次不等式组,解之即可得出
的一元一次不等式组,解之即可得出![]() 的取值范围,由此即可得出各进货方案;
的取值范围,由此即可得出各进货方案;
解:(1)设橱具店购进电饭煲![]() 台,电压锅
台,电压锅![]() 台,
台,
根据题意得:![]() 解得:
解得:![]()
∴![]() (元)。
(元)。
答:橱具店在该买卖中赚了1400元。
(2)设购买电饭煲![]() 台,则购买电压锅
台,则购买电压锅![]() 台,
台,
根据题意得:
解得:![]() 。
。
又∵![]() 为正整数。
为正整数。
∴![]() 可取23,24,25.
可取23,24,25.
故有三种方案:①鹏买电饭煲23台,购买电压锅27台;②购买电饭煲24台,电压锅26台;③购买电饭煲25台。购买电压锅25台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)阅读理解:课外兴趣小组活动时,老师提出了如下问题:
在△ABC中,AB=9,AC=5,求BC边上的中线AD的取值范围。
小明在组内经过合作交流,得到了如下的解决方法(如图1):
①延长AD到Q,使得DQ=AD;
②再连接BQ,把AB、AC、2AD集中在△ABQ中;
③利用三角形的三边关系可得4<AQ<14,则AD的取值范围是_____________。
感悟:解题时,条件中若出现“中点”“中线”等条件,可以考虑倍长中线,构造全等三角形,把分散的己知条件和所求证的结论集中到同一个三角形中。
(2)请你写出图1中AC与BQ的位置关系并证明。
(3)思考:已知,如图2,AD是△ABC的中线,AB=AE,AC=AF,∠BAE=∠FAC=90°。试探究线段AD与EF的数量和位置关系并加以证明。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在水平地面点A处有一网球发射器向空中发射网球,网球飞行路线是一条抛物线,在地面上落点为B,有人在直线AB上点C(靠点B一侧)竖直向上摆放若干个无盖的圆柱形桶.试图让网球落入桶内,已知AB=4米,AC=3米,网球飞行最大高度OM=5米,圆柱形桶的直径为0.5米,高为0.3米(网球的体积和圆柱形桶的厚度忽略不计).当竖直摆放圆柱形桶至少________个时,网球可以落入桶内.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,A点的坐标为(0,3),B点的坐标为(-3.0),D为x轴上的一个动点,AE⊥AD,且AE=AD,连接BE交y轴于点M
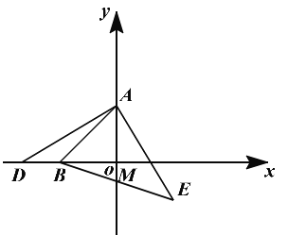
(1)若D点的坐标为(-5.0),求E点的坐标:
(2)求证:M为BE的中点
(3)当D点在x轴上运动时,探索:
 为定值
为定值 -
科目: 来源: 题型:
查看答案和解析>>【题目】下列各比值中,是直角三角形的三边之比的是( )
A.
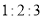 B.
B.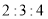 C.
C.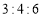 D.3:4:5
D.3:4:5 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,菱形ABCD的边长为2,
 ,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.
,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数
众数
中位数
方差
甲
8
8
0.4
乙
9
3.2
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
相关试题

