【题目】如图,菱形ABCD的边长为2,![]() ,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.
,点E为BC边的中点,点P为对角线AC上一动点,则PB+PE的最小值为_____.

参考答案:
【答案】![]()
【解析】
根据ABCD是菱形,找出B点关于AC的对称点D,连接DE交AC于P,则DE就是PB+PE的最小值,根据勾股定理求出即可.
解:如图,连接DE交AC于点P,连接DB,
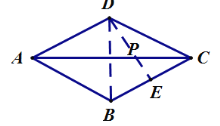
∵四边形ABCD是菱形,
∴点B、D关于AC对称(菱形的对角线相互垂直平分),
∴DP=BP,
∴PB+PE的最小值即是DP+PE的最小值(等量替换),
又∵ 两点之间线段最短,
∴DP+PE的最小值的最小值是DE,
又∵![]() ,CD=CB,
,CD=CB,
∴△CDB是等边三角形,
又∵点E为BC边的中点,
∴DE⊥BC(等腰三角形三线合一性质),
菱形ABCD的边长为2,
∴CD=2,CE=1,
由勾股定理得![]() ,
,
故答案为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线
 的顶点坐标为
的顶点坐标为 ,并且与
,并且与 轴交于点
轴交于点 ,与
,与 轴交于
轴交于 、
、 两点.
两点.(
 )求抛物线的表达式.
)求抛物线的表达式.(
 )如图
)如图 ,设抛物线的对称轴与直线
,设抛物线的对称轴与直线 交于点
交于点 ,点
,点 为直线
为直线 上一动点,过点
上一动点,过点 作
作 轴的平行线
轴的平行线 ,与抛物线交于点
,与抛物线交于点 ,问是否存在点
,问是否存在点 ,使得以
,使得以 、
、 、
、 为顶点的三角形与
为顶点的三角形与 相似.若存在,求出点
相似.若存在,求出点 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
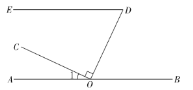
查看答案和解析>>【题目】如图,点O在直线AB上,OC⊥OD,∠EDO与∠1互余.
(1)求证:ED//AB;
(2)OF平分∠COD交DE于点F,若∠OFD=65°,补全图形,并求∠1的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在矩形ABCD中,
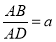 ,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.
,点G,H分别在边AB,DC上,且HA=HG,点E为AB边上的一个动点,连接HE,把△AHE沿直线HE翻折得到△FHE.(1)如图1,当DH=DA时,
①填空:∠HGA= 度;
②若EF∥HG,求∠AHE的度数,并求此时a的最小值;
(2)如图3,∠AEH=60°,EG=2BG,连接FG,交边FG,交边DC于点P,且FG⊥AB,G为垂足,求a的值.

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读与探究
我们给出如下定义:若一个四边形中存在相邻两边的平方和等于一条对角线的平方,则称这个四边形为勾股四边形,这两条相邻的边称为这个四边形的勾股边.请结合上述阅读材料,解决下列问题:

 在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可);
在我们所学过的特殊四边形中,是勾股四边形的是________ (任写一种即可); 图1、图2均为
图1、图2均为 的正方形网格,点
的正方形网格,点 均在格点上,请在图中标出格点
均在格点上,请在图中标出格点 ,连接
,连接 ,使得四边形
,使得四边形 符合下列要求:图1中的四边形
符合下列要求:图1中的四边形 是勾股四边形,并且是轴对称图形;图2中的四边形
是勾股四边形,并且是轴对称图形;图2中的四边形 是勾股四边形且对角线相等,但不是轴对称图形.
是勾股四边形且对角线相等,但不是轴对称图形. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,四边形
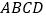 中,
中, ,
, ,
, ,且
,且 ,
,试求:(1)
 的度数;(2)四边形
的度数;(2)四边形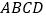 的面积(结果保留根号);
的面积(结果保留根号);
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:在边长为
 的正方形
的正方形 中,对角线
中,对角线 、
、 交于点
交于点 .
.探究
 :如图
:如图 ,若点
,若点 是对角线
是对角线 上任意一点,则线段
上任意一点,则线段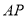 的长的取值范围是__________;
的长的取值范围是__________;探究
 :如图
:如图 ,若点
,若点 是
是 内任意一点,点
内任意一点,点 、
、 分别是
分别是 边和对角线
边和对角线 上的两个动点,则当
上的两个动点,则当 的值在探究
的值在探究 中的取值范围内变化时,
中的取值范围内变化时,  的周长是否存在最小值?如果存在,请求出
的周长是否存在最小值?如果存在,请求出 周长的最小值,若不存在,请说明理由;
周长的最小值,若不存在,请说明理由;问题解决:如图
 ,在边长为
,在边长为 的正方形
的正方形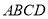 中,点
中,点 是
是 内任意一点,且
内任意一点,且 ,点
,点 、
、 分别是
分别是 边和对角线
边和对角线 上的两个动点,则当
上的两个动点,则当 的周长取到最小值时,求四边形
的周长取到最小值时,求四边形 面积的最大值.
面积的最大值.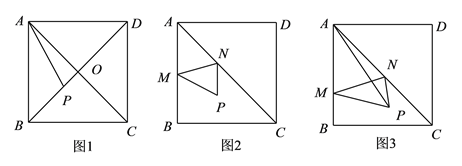
相关试题

