【题目】甲、乙两人在5次打靶测试中命中的环数如下:
甲:8,8,7,8,9
乙:5,9,7,10,9
(1)填写下表:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | | 8 | 0.4 |
乙 | | 9 | | 3.2 |
(2)教练根据这5次成绩,选择甲参加射击比赛,教练的理由是什么?
(3)如果乙再射击1次,命中8环,那么乙的射击成绩的方差 .(填“变大”、“变小”或“不变”).
参考答案:
【答案】(1)填表见解析;(2)理由见解析;(3)变小.
【解析】试题分析:(1)根据众数、平均数和中位数的定义求解:甲的众数为8,乙的平均数=![]() (5+9+7+10+9)=8,乙的中位数为9.
(5+9+7+10+9)=8,乙的中位数为9.
(2)方差就是和中心偏离的程度,用来衡量一批数据的波动大小(即这批数据偏离平均数的大小)在样本容量相同的情况下,方差越大,说明数据的波动越大,越不稳定.
(3)根据方差公式求解:如果乙再射击1次,命中8环,那么乙的射击成绩的方差变小.
试题解析:解:(1)填表如下:
平均数 | 众数 | 中位数 | 方差 | |
甲 | 8 | 8 | 8 | 0.4 |
乙 | 8 | 9 | 9 | 3.2 |
(2)因为他们的平均数相等,而甲的方差小,发挥比较稳定,所以选择甲参加射击比赛;
(3)变小.
-
科目: 来源: 题型:
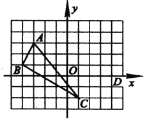
查看答案和解析>>【题目】在平面直角坐标系中, △ABC三个顶点的位置如图(每个小正方形的边长均为1).
(1)请画出△ABC沿x轴向右平移3个单位长度,再沿y轴向上平移2个单位长度后的△A′B′C′(其中A′、B′、C′分别是A、B、C的对应点,不写画法)
(2)直接写出A′、B′、C′三点的坐标: A′(_____,______); B′(_____,______); C′(_____,______)。
(3)求△ABC的面积。
-
科目: 来源: 题型:
查看答案和解析>>【题目】为深化义务教育课程改革,满足学生的个性化学习需求,某校就“学生对知识拓展、体育特长、艺术特长和时间活动四类选课意向”进行了抽样调查(每人选报一类),绘制了如图所示的两幅统计图(不完整),请根据图中信息,解答下列问题.
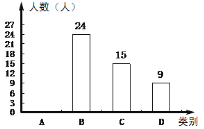
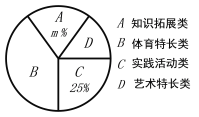
(1)求扇形统计图中的m的值,并补全条形统计图;
(2)已知该校800名学生,计划开设“实践活动类”课程,每班安排20人,问学校开设多少个“实践活动课”课程的班级比较合理.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在
 中,
中, ,
, 平分
平分 ,
, 于点
于点 交
交 于
于 点,延长
点,延长 至
至 使
使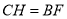 ,连接
,连接 .
.
(1)证明:四边形
 是矩形;
是矩形;(2)当
 时,猜想线段
时,猜想线段 、
、 、
、 的数量关系,并证明.
的数量关系,并证明. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y1=ax2+2x+c与直线y2=kx+b交于点A(-1,0)、B(2,3).
(1)求a、b、c的值;
(2)直接写出当y1<y2时,自变量的范围是__________________________.
(3)若点C是抛物线的顶点,求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知菱形
 的周长为
的周长为 ,两个邻角
,两个邻角 与
与 的比是
的比是 ,则这个菱形的面积是__________.
,则这个菱形的面积是__________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,⊙P经过x轴上一点C,与y轴分别相交于A、B两点,连接AP并延长分别交⊙P、x轴于点D、点E,连接DC并延长交y轴于点F.若点F的坐标为
 ,点D的坐标为
,点D的坐标为 .
.(1)求证:DC=FC;
(2)判断⊙P与x轴的位置关系,并说明理由;
(3)求⊙P的半径.

相关试题

