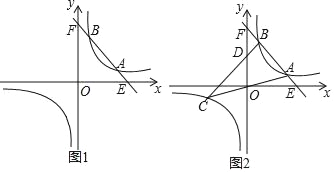
【题目】已知:一次函数y=﹣2x+10的图象与反比例函数y=![]() (k>0)的图象相交于A、B两点(A的B的右侧).
(k>0)的图象相交于A、B两点(A的B的右侧).
(1)当A(4,2)时,求反比例函数的解析式:
(2)当A的横坐标是3,B的横坐标是2时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.
①求C点的坐标;
②求D点的坐标;
③求△ABC的面积.
参考答案:
【答案】(1)![]() ;(2)① C(﹣3,﹣4),B(2,6);②D点的坐标为(2,2);③10.
;(2)① C(﹣3,﹣4),B(2,6);②D点的坐标为(2,2);③10.
【解析】(1)依据反比例函数y=![]() (k>0)图象经过A(4,2),即可得到反比例函数的解析式为:=
(k>0)图象经过A(4,2),即可得到反比例函数的解析式为:=![]() ;
;
(2) ①依据一次函数y=-2x+10的图象经过A、B两点,可得A(3,4),即可得到C(-3,-4);②利用待定系数法可得直线BC的解析式为y=2x+2,进而得出D点坐标为(2,2);③依据△ABC的面积=![]() 进行计算.
进行计算.
(1)∵反比例函数y=![]() (k>0)的图象经过A(4,2),
(k>0)的图象经过A(4,2),
∴k=4×2=8,
∴反比例函数的解析式为:y=![]() ;
;
(2)①∵一次函数y=﹣2x+10的图象经过A、B两点,A的横坐标是3,B的横坐标是2,
∴当x=3时,y=4;当x=2时,y=6,
∴A(3,4),
又∵直线OA与此反比例函数图象的另一支交于另一点C,
∴C(﹣3,﹣4),B(2,6);
②设直线BC的解析式为y=ax+b,则
![]() ,
,
解得![]() ,
,
∴直线BC的解析式为y=2x+2,
∴令x=2,则y=2,
∴D点的坐标为(2,2);
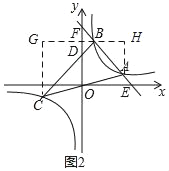
③△ABC的面积=S梯形ACGH﹣S△BCG﹣S△ABH
=![]() (2+10)×6﹣
(2+10)×6﹣![]() ×10×5﹣
×10×5﹣![]() ×2×1
×2×1
=36﹣25﹣1
=10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】弹簧挂上物体后会伸长,测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系,那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )

A. y=x+12 B. y=0.5x+12
C. y=0.5x+10 D. y=x+10.5
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简再求值:
(1)[(xy+2)(xy﹣2)﹣2x2y2+4]÷(xy),其中x=10,y=
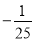
(2)(x+2y)2﹣(x+y)(3x﹣y)﹣5y2,其中x=﹣2,y=
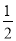
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点D是⊙O的直径CA延长线上一点,点B在⊙O上,且∠DBA=∠BCD.
(1)证明:BD是⊙O的切线.
(2)若点E是劣弧BC上一点,AE与BC相交于点F,且△BEF的面积为16,cos∠BFA=
 ,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.
,那么,你能求出△ACF的面积吗?若能,请你求出其面积;若不能,请说明理由.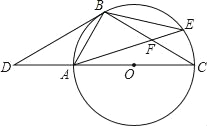
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线y=﹣
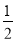 x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求m和b的数量关系;
(2)当m=1时,如图2,将△BCD沿x轴正方向平移得△B′C′D′,当直线B′C′经过点D时,求点B′的坐标及△BCD平移的距离;
(3)在(2)的条件下,直线AB上是否存在一点P,以P、C、D为顶点的三角形是等腰直角三角形?若存在,写出满足条件的P点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=
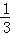 AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.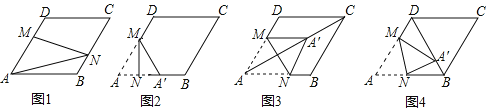
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求
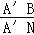 的值.
的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数
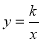 (k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.
(k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.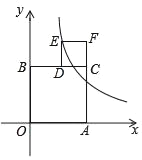
相关试题

