搜索
【题目】先化简再求值：
（1）[（xy+2）（xy﹣2）﹣2x2y2+4]÷（xy），其中x＝10，y＝
（2）（x+2y）2﹣（x+y）（3x﹣y）﹣5y2，其中x＝﹣2，y＝
参考答案：
【答案】（1）﹣xy，
；（2）﹣2x2+2xy，﹣10
【解析】
（1）根据整式的运算法则进行化简，然后将x与y的值代入原式即可求出答案；
（2）根据整式的运算法则进行化简，然后将x与y的值代入原式即可求出答案；
解：（1）原式＝（x2y2﹣4﹣2x2y2+4）÷（xy）
＝（﹣x2y2）÷（xy）
＝﹣xy，
当x＝10，y＝
时，
原式＝；
故答案为：﹣xy，；
（ 2 ）原式＝x2+4xy+4y2﹣（3x2+2xy﹣y2）﹣5y2
＝﹣2x2+2xy，
当x＝﹣2，y＝
时，
原式＝﹣10，
故答案为：﹣2x2+2xy，﹣10．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（新定义）：A、B、C 为数轴上三点，若点 C 到 A 的距离是点 C 到 B 的距离的 3 倍，我们就称点
C 是（A，B）的幸运点．
（特例感知）：
（1）如图 1，点 A 表示的数为﹣1，点 B 表示的数为 3．表示 2 的点 C 到点 A 的距离是 3， 到点 B 的距离是 1，那么点 C 是（A，B）的幸运点．
①（B，A）的幸运点表示的数是 ；A．﹣1； B.0； C.1； D.2
②试说明 A 是（C，E）的幸运点．
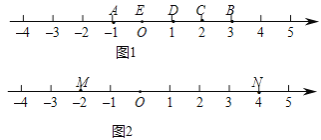
（2）如图 2，M、N 为数轴上两点，点 M 所表示的数为﹣2，点 N 所表示的数为 4，则（M，N）的幸点示的数为 ．
（拓展应用）：
（3）如图 3，A、B 为数轴上两点，点 A 所表示的数为﹣20，点 B 所表示的数为 40．现有一只电子蚂蚁 P 从点 B 出发，以 3 个单位每秒的速度向左运动，到达点 A 停止．当 t 为何值时，P、A 和 B 三个点中恰好有一个点为其余两点的幸运点？
-
科目： 来源： 题型：
查看答案和解析>>【题目】初二年级教师对试卷讲评课中学生参与的深度与广度进行评价调查，其评价项目为主动质疑、独立思考、专注听讲、讲解题目四项．评价组随机抽取了若干名初二学生的参与情况，绘制成如图所示的频数分布直方图和扇形统计图（均不完整），请根据图中所给信息解答下列问题：
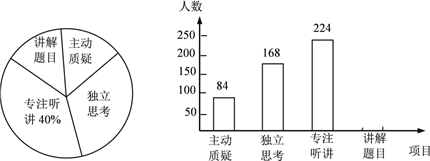
（1）在这次评价中，一共抽查了 名学生；
（2）在扇形统计图中，项目“主动质疑”所在的扇形的圆心角的度数为 度；
（3）请将频数分布直方图补充完整；
（4）如果全市有6000名初二学生，那么在试卷评讲课中，“独立思考”的初二学生约有多少人？
-
科目： 来源： 题型：
查看答案和解析>>【题目】弹簧挂上物体后会伸长，测得一弹簧的长度y(cm)与所挂重物的质量x(kg)有下面的关系，那么弹簧总长y(cm)与所挂重物x(kg)之间的关系式为( )
A. y＝x＋12 B. y＝0.5x＋12
C. y＝0.5x＋10 D. y＝x＋10.5
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，点D是⊙O的直径CA延长线上一点，点B在⊙O上，且∠DBA=∠BCD．
（1）证明：BD是⊙O的切线．
（2）若点E是劣弧BC上一点，AE与BC相交于点F，且△BEF的面积为16，cos∠BFA=
，那么，你能求出△ACF的面积吗？若能，请你求出其面积；若不能，请说明理由．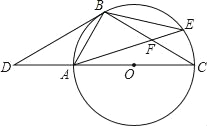
-
科目： 来源： 题型：
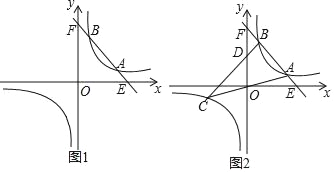
查看答案和解析>>【题目】已知：一次函数y=﹣2x+10的图象与反比例函数y=
（k＞0）的图象相交于A、B两点（A的B的右侧）．（1）当A（4，2）时，求反比例函数的解析式：
（2）当A的横坐标是3，B的横坐标是2时，直线OA与此反比例函数图象的另一支交于另一点C，连接BC交y轴于点D．
①求C点的坐标；
②求D点的坐标；
③求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1，在平面直角坐标系中，直线y＝﹣
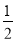x+b与x轴、y轴相交于A、B两点，动点C（m，0）在线段OA上，将线段CB绕着点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上，过点D作DE⊥x轴于点E．（1）求m和b的数量关系；
（2）当m＝1时，如图2，将△BCD沿x轴正方向平移得△B′C′D′，当直线B′C′经过点D时，求点B′的坐标及△BCD平移的距离；
（3）在（2）的条件下，直线AB上是否存在一点P，以P、C、D为顶点的三角形是等腰直角三角形？若存在，写出满足条件的P点坐标；若不存在，请说明理由．
相关试题
