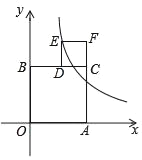
【题目】如图,四边形AOBC和四边形CDEF都是正方形,边OA在x轴上,边OB在y轴上,点D在边CB上,反比例函数![]() (k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.
(k>0)在第一象限的图象经过点E,若正方形AOBC和正方形CDEF的面积之差为6,则k=_____.
参考答案:
【答案】6
【解析】
设出正方形AOBC的边长为与正方形CDEF的边长,表示出E点,然后E点在反比例函数上,直接代入,利用面积直接解出k即可
解:设正方形AOBC的边长为a,正方形CDEF的边长为b,则E(a﹣b,a+b),
∵反比例函数的图象经过点E,
∴(a+b)(a﹣b)=k,
整理为a2﹣b2=k,
∵S正方形AOBC=a2,S正方形CDEF=b2,
∴S正方形AOBC﹣S正方形CDEF=6,
即a2﹣b2=6,
∴k=6,
故答案为:6
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:一次函数y=﹣2x+10的图象与反比例函数y=
 (k>0)的图象相交于A、B两点(A的B的右侧).
(k>0)的图象相交于A、B两点(A的B的右侧).(1)当A(4,2)时,求反比例函数的解析式:
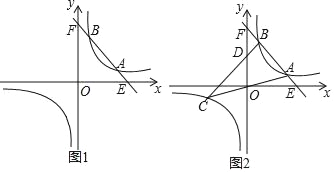
(2)当A的横坐标是3,B的横坐标是2时,直线OA与此反比例函数图象的另一支交于另一点C,连接BC交y轴于点D.
①求C点的坐标;
②求D点的坐标;
③求△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,直线y=﹣
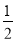 x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.
x+b与x轴、y轴相交于A、B两点,动点C(m,0)在线段OA上,将线段CB绕着点C顺时针旋转90°得到CD,此时点D恰好落在直线AB上,过点D作DE⊥x轴于点E.(1)求m和b的数量关系;
(2)当m=1时,如图2,将△BCD沿x轴正方向平移得△B′C′D′,当直线B′C′经过点D时,求点B′的坐标及△BCD平移的距离;
(3)在(2)的条件下,直线AB上是否存在一点P,以P、C、D为顶点的三角形是等腰直角三角形?若存在,写出满足条件的P点坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在图1﹣﹣图4中,菱形ABCD的边长为3,∠A=60°,点M是AD边上一点,且DM=
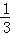 AD,点N是折线AB﹣BC上的一个动点.
AD,点N是折线AB﹣BC上的一个动点.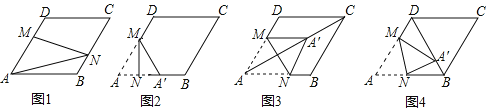
(1)如图1,当N在BC边上,且MN过对角线AC与BD的交点时,则线段AN的长度为 .
(2)当点N在AB边上时,将△AMN沿MN翻折得到△A′MN,如图2,
①若点A′落在AB边上,则线段AN的长度为 ;
②当点A′落在对角线AC上时,如图3,求证:四边形AM A′N是菱形;
③当点A′落在对角线BD上时,如图4,求
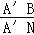 的值.
的值. -
科目: 来源: 题型:
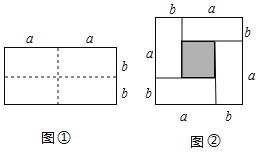
查看答案和解析>>【题目】(1)如图①是一个长为2a,宽为2b的长方形,若将此图中虚线用剪刀均分为四块小长方形,然后按图②的形状拼成一个正方形,请问:这两个图形的什么量不变?请填写这个量的名称 .所得的正方形的面积比原长方形的面积多出的阴影部分的面积用含a,b的代数式表示 ;
(2)由①的探索中,可以得出的结论是:在周长一定的长方形中,当 时,面积最大;
(3)若一长方形的周长为36厘米,则当边长为多少时,该图形的面积最大?最大面积是多少?
-
科目: 来源: 题型:
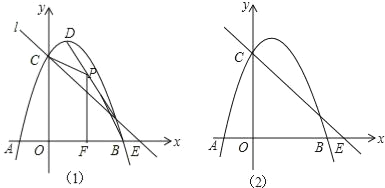
查看答案和解析>>【题目】如图1,抛物线y=﹣x2+2x+3与x轴交于A,B,与y轴交于C,抛物线的顶点为D,直线l过C交x轴于E(4,0).
(1)写出D的坐标和直线l的解析式;
(2)P(x,y)是线段BD上的动点(不与B,D重合),PF⊥x轴于F,设四边形OFPC的面积为S,求S与x之间的函数关系式,并求S的最大值;
(3)点Q在x轴的正半轴上运动,过Q作y轴的平行线,交直线l于M,交抛物线于N,连接CN,将△CMN沿CN翻转,M的对应点为M′.在图2中探究:是否存在点Q,使得M′恰好落在y轴上?若存在,请求出Q的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】“单词的记忆效率”是指复习一定量的单词,一周后能正确默写出的单词个数与复习的单词个数的比值.右图描述了某次单词复习中
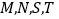 四位同学的单词记忆效率
四位同学的单词记忆效率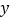 与复习的单词个数
与复习的单词个数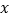 的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )
的情况,则这四位同学在这次单词复习中正确默写出的单词个数最多的是( )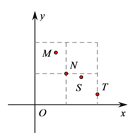
A.
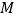 B.
B. 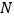 C.
C. 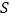 D.
D. 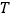
相关试题

