【题目】某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )
![]()
A.A区B.B区C.C区D.A.B两区之间
参考答案:
【答案】A
【解析】
根据题意分别计算停靠点分别在A、B、C各点和A区、B区之间时员工步行的路程和,选择最小的即可求解.
解:∵当停靠点在A区时,所有员工步行到停靠点路程和是:
15×100+10×300=4500m,
当停靠点在B区时,所有员工步行到停靠点路程和是:30×100+10×200=5000m,
当停靠点在C区时,所有员工步行到停靠点路程和是:30×300+15×200=12000m,
当停靠点在A、B区之间时,
设在A区、B区之间时,设距离A区x米,
则所有员工步行路程之和=30x+15(100-x)+10(100+200-x),
=30x+1500-15x+3000-10x,
=5x+4500,
∴当x=0时,即在A区时,路程之和最小,为4500米;
综上,当停靠点在A区时,所有员工步行到停靠点路程和最小,那么停靠点的位置应该在A区.
故选:A.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1

图2

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥CD,分别探究下面三个图形中∠P和∠A,∠C的关系,请你从所得三个关系中任意选出一个,说明你探究结论的正确性.
结论:(1)___________________;
(2)____________________;
(3)_____________________;
(4)选择结论____________,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )个棋子.

A.159B.169C.172D.132
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

-
科目: 来源: 题型:
查看答案和解析>>【题目】为了了解龙岗区学生喜欢球类活动的情况,采取抽样调查的方法,从足球、乒乓球、篮球、排球等四个方面调查了全班学生的兴趣爱好,根据调查的结果绘制成如图所示的两幅不完整的统计图(如图①,②,要求每位学生只能选择一种自己喜欢的球类),请你根据图中提供的信息解答下列问题:
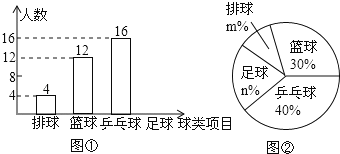
(1)本次共调查的学生人数为___,并把条形统计图补充完整;
(2)扇形统计图中m=___,n=___;
(3)表示“足球”的扇形的圆心角是___度;
(4)若龙岗区初中学生共有60000人,则喜欢乒乓球的有多少人.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,已知OB,OC是∠AOD内部的两条射线,OM平分∠AOB,ON平分∠COD.
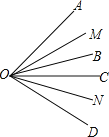
(1)若∠BOC=25°,∠MOB=15°,∠NOD=10°,求∠AOD的大小;
(2)若∠AOD=75°,∠MON=55°,求∠BOC的大小;
(3)若∠AOD=α,∠MON=β,求∠BOC的大小(用含α,β的式子表示).
相关试题

