【题目】如图,已知AB∥CD,分别探究下面三个图形中∠P和∠A,∠C的关系,请你从所得三个关系中任意选出一个,说明你探究结论的正确性.
结论:(1)___________________;
(2)____________________;
(3)_____________________;
(4)选择结论____________,说明理由.

参考答案:
【答案】(1)∠APC+∠PAB+∠PCD=360°;(2)∠APC=∠PAB+∠PCD;(3)∠PCD=∠APC+∠PAB;(4)∠APC+∠PAB+∠PCD=360°,理由见解析.
【解析】
(1)过点P作PE∥AB,则AB∥PE∥CD,再根据两直线平行,同旁内角互补即可解答;
(2)过点P作PF∥AB,则AB∥CD∥PF,再根据两直线平行,内错角相等即可解答;
(3)根据AB∥CD,可得出∠1=∠PCD,再根据三角形外角的性质进行解答;
(4)选择以上结论任意一个进行证明即可.
解:(1)过点P作PE∥AB,则AB∥PE∥CD,
∴∠1+∠PAB=180°,
∠2+∠PCD=180°,
∴∠APC+∠PAB+∠PCD=360°.
故答案为:∠APC+∠PAB+∠PCD=360°;
(2)过点P作直线PF∥AB,
∵AB∥CD,
∴AB∥PF∥CD,
∴∠PAB=∠1,∠PCD=∠2,
∴∠APC=∠PAB+∠PCD.
故答案为:∠APC=∠PAB+∠PCD;
(3)∵AB∥CD,
∴∠1=∠C,
∵∠1=∠PAB+∠APC,
∴∠PCD=∠APC+∠PAB.
故答案为:∠PCD=∠APC+∠PAB.
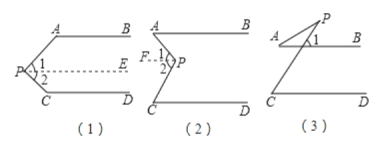
(4)选择结论∠APC+∠PAB+∠PCD=360°
理由:过点P作PE∥AB,则AB∥PE∥CD,
∴∠1+∠PAB=180°,
∠2+∠PCD=180°,
∴∠APC+∠PAB+∠PCD=360°
故答案为:∠APC+∠PAB+∠PCD=360°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线y=ax2+bx+
 经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.
经过A(1,0),B(7,0)两点,交y轴于D点,以AB为边在x轴上方作等边三角形ABC.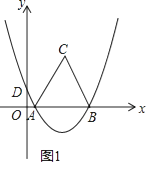
(1)求抛物线的解析式;
(2)在x轴上方的抛物线上是否存在点M,是S△ABM=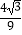 S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
S△ABC?若存在,请求出点M的坐标;若不存在,请说明理由;
(3)如图2,E是线段AC上的动点,F是线段BC上的动点,AF与BE相交于点P.
①若CE=BF,试猜想AF与BE的数量关系及∠APB的度数,并说明理由;
②若AF=BE,当点E由A运动到C时,请直接写出点P经过的路径长.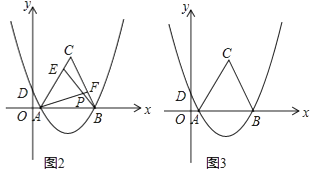
-
科目: 来源: 题型:
查看答案和解析>>【题目】关于x的一元二次方程ax2﹣3x+3=0有两个不等实根,则a的取值范围是( )
A.a< 且a≠0
且a≠0
B.a>﹣ 且a≠0
且a≠0
C.a>﹣
D.a<
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,将矩形纸片ABCD沿对角线BD向上折叠,点C落在点E处,BE交AD于点F.
(1)求证:△BDF是等腰三角形;
(2)如图2,过点D作DG∥BE,交BC于点G,连接FG交BD于点O.
①判断四边形BFDG的形状,并说明理由;
②若AB=6,AD=8,求FG的长.
图1

图2

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小华用黑白棋子组成的一组图案,第1个图案由1个黑子组成,第2个图案由1个黑子和6个白子组成,第3个图案由13个黑子和6个白子组成,按照这样的规律排列下去,则第8个图案中共有( )个棋子.

A.159B.169C.172D.132
-
科目: 来源: 题型:
查看答案和解析>>【题目】某公司员工分别在A、B、C三个住宅区,A区有30人,B区有15人,C区有10人,三个区在一条直线上,位置如图所示,该公司的接送车打算在此间只设一个停靠点,为使所有员工步行到停靠点的路程之和最小,那么停靠点的位置应设在( )

A.A区B.B区C.C区D.A.B两区之间
-
科目: 来源: 题型:
查看答案和解析>>【题目】“中华人民共和国道路交通管理条例”规定:小汽车在城市街道上行驶速度不得超过70 km/h.如图,一辆小汽车在一条城市街路上直道行驶,某一时刻刚好行驶到路对面车速检测仪正前方30 m处,过了2 s后,测得小汽车与车速检测仪间距离为50 m,这辆小汽车超速了吗?

相关试题

