【题目】如图,在Rt△ABC中,∠ACB=90°,BC=3,AC=4,G是边AB的中点,平行于AB的动直线l分别交△ABC的边CA、CB于点M、N,设CM=m.
(1)当m=1时,求△MNG的面积;
(2)若点G关于直线l的对称点为点G′,请求出点G′ 恰好落在△ABC的内部(不含边界)时,m的取值范围;
(3)△MNG是否可能为直角三角形?如果能,请求出所有符合条件的m的值;如果不能,请说明理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() <m<4;(3)能,m=2或
<m<4;(3)能,m=2或![]()
【解析】分析:(1)由l//AB可证△CMN∽△CAB利用相似的性质即可求出△MNG的边MN及MN边上的高,利用三角形的面积公式即可得出答案;
(2)根据点G关于直线l的对称点G′分别落在AB边、AC边时的m值,即可求出m的取值范围;
(3)分三种情况讨论(△MNG的三个内角分别为90°),即可得出答案.
详解:(1)当m=1时,S△MNG=![]() =
=![]() .
.
(2)当点G关于直线l的对称点G′落在AB边时,m=4,
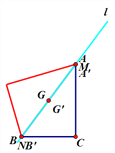
当点G关于直线l的对称点G′落在AC边时,点M是AG′的中点,
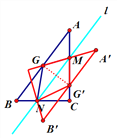
由△AGG′∽△ACB,
可求AG′=![]() ,
,
∴CM=m=4-![]() =
=![]() ,
,
∴点G′恰好落在△ABC的内部(不含边界)时,![]() <m<4,
<m<4,
(3)△MNG能为直角三角形,
①当∠MGN=90°时,
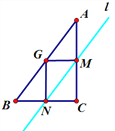
证得四边形CMGN为矩形,
∴M是AC的中点,
∴m=2,
②当∠GMN=90°时,
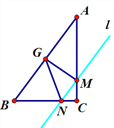
![]() =
=![]() ,
,
m=![]() ,
,
③当∠GNM=90°时,![]() =
=![]() ,
,
m=-![]() (不合题意,舍去),
(不合题意,舍去),
∴m=2或m=![]() 时,△MNG是直角三角形.
时,△MNG是直角三角形.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+k﹣2经过点(m,n+1)和(m+1,2n+3),且﹣2<k<0,则n的取值范围是( )
A. ﹣2<n<0B. ﹣4<n<﹣2C. ﹣4<n<0D. 0<n<﹣2
-
科目: 来源: 题型:
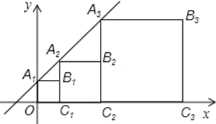
查看答案和解析>>【题目】彼此相似的矩形A1B1C1O,A2B2C2C1,A3B3C3C2,…,按如图所示的方式放置.点A1,A2,A3,…,和点C1,C2,C3,…,分别在直线y=kx+b(k>0)和x轴上,已知点B1、B2的坐标分别为(1,2),(3,4),则Bn的坐标是( )
A. (2n﹣1,2n)B. (2n﹣
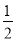 ,2n)
,2n)C. (2n﹣1﹣
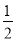 ,2n﹣1)D. (2n﹣1﹣1,2n﹣1)
,2n﹣1)D. (2n﹣1﹣1,2n﹣1) -
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形ABCD中,点E,F分别在边BC,CD上,且∠EAF=∠CEF=45°.
(1)将△ADF绕着点A顺时针旋转90°,得到△ABG(如图①),求证:△AEG≌△AEF;
(2)若直线EF与AB,AD的延长线分别交于点M,N(如图②),求证:EF2=ME2+NF2;
(3)将正方形改为长与宽不相等的矩形,若其余条件不变(如图③),请你直接写出线段EF,BE,DF之间的数量关系.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)求多项式4x2﹣3﹣6x与多项式﹣x2+2x+5的2倍的和.
(2)先化简,再求值:
 ,其中
,其中
(3)已知两个多项式A,B,其中B=﹣2x2+5x﹣3,求A﹣B.小马虎同学在计算时,误将A﹣B错看成了A+B,求得的结果为3x2﹣2x+10.请你帮助这位同学求出正确结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】九年级数学兴趣小组经过市场调查,得到某种运动服每月的销量与售价的相关信息如下表:
售价(元/件)
100
110
120
130
……
月销量(件)
200
180
160
140
……
(1)已知该运动服的进价为每件60元,设售价为x元;
请用含有x的式子表示:
①销售该运动服每件的利润是 元;
②月销售量是 件;(直接写结果)
(2)设销售该运动服的月利润为y元,那么售价为多少元时,当月的利润最大?最大利润是多少?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上两点A.B对应的数分别为﹣2和7,点M为数轴上一动点.
(1)请画出数轴,并在数轴上标出点A、点B;
(2)若点M到A的距离是点M到B的距离的两倍,我们就称点M是(A,B)的好点.
①若点M运动到原点O时,此时点M (A,B)的好点(填是或者不是)
②若点M以每秒1个单位的速度从原点O开始运动,当M是(B,A)的好点时,求点M的运动方向和运动时间
(3)试探究线段BM和AM的差即BM﹣AM的值是否一定发生变化?若变化,请说明理由:若不变,请求其值.
相关试题

