【题目】如图,在矩形![]() 纸片中,
纸片中,![]() cm,
cm,![]() cm。点
cm。点![]() 在
在![]() 边上,将
边上,将![]() 沿
沿![]() 折叠,得
折叠,得![]() ,连接
,连接![]() ,
, ![]() .
.
(1)当点![]() 落在
落在![]() 边上时,
边上时,![]() ;
;
(2)当点![]() 是
是![]() 的中点时,求
的中点时,求![]() 的长;
的长;
(3)当![]() 分别满足下列条件时,求相应的
分别满足下列条件时,求相应的![]() 的长:
的长:
①![]() ;②
;②![]() .
.
参考答案:
【答案】(1)2![]() ; (2)
; (2)![]() ;(3)①
;(3)①![]() ;②
;②![]() .
.
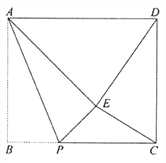
【解析】(1)如图1,根据已知条件得到四边形ABPE是正方形,求得PC=2,根据勾股定理得到CE的长;
(2)如图2,取CE的中点F,连接PF,由点P是BC的中点,得到PB=PC=6,根据勾股定理得到PA的长,根据折叠的性质得到∠APE=∠APB,PE=PB=6, PC=PE,根据等腰三角形的性质得到∠EPF=∠CPF,∠PFC=90°,CE=2CF,由余角的性质得到∠CPF=∠PAB,根据相似三角形的得到CF的长,于是得到结论;
(3)①如图3,过E作MN⊥AD于M,交BC于N,则MN⊥BC,根据勾股定理得到ME的长,求得EN=MN﹣ME=2,根据相似三角形的性质得到PB的长;
②如图3,过E作EQ⊥CD于Q,根据勾股定理和相似三角形的性质即可得到结论.
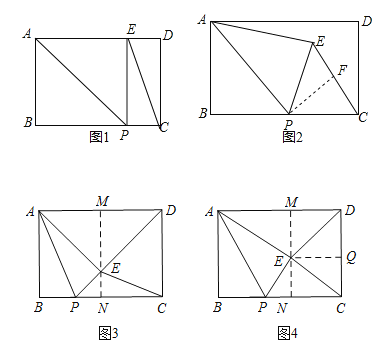
(1)如图1.∵将△PAB沿AP折叠,得△PAE,∴四边形ABPE是正方形,
∴PB=PE=AB=10,∴PC=2,∴CE=![]() =2
=2![]() .
.
故答案为:2![]() ;
;
(2)如图2,取CE的中点F,连接PF.
∵点P是BC的中点,∴PB=PC=6.
∵AB=10,∴PA=![]() =2
=2![]() .
.
∵将△PAB沿AP折叠,得△PAE,∴∠APE=∠APB,PE=PB=6,∴PC=PE.
∵点F是CE的中点,∴∠EPF=∠CPF,∠PFC=90°,CE=2CF,∴∠APF=90°,∴∠APB+∠CPF=∠APB+∠PAB=90°,∴∠CPF=∠PAB,∴△PAB∽△CPF,∴![]() ,∴CF=
,∴CF=![]() ,∴CE=2CF=
,∴CE=2CF=![]() ;
;
(3)①如图3,过E作MN⊥AD于M,交BC于N,则MN⊥BC.
∵DE=CD,AE=AB=CD=DE,∴AE=10,∴AM=![]() AD=6=BN,∴ME=
AD=6=BN,∴ME=![]() =8,∴EN=MN﹣ME=2,易知,△AME∽△ENP,∴
=8,∴EN=MN﹣ME=2,易知,△AME∽△ENP,∴![]() ,∴PE=PB=
,∴PE=PB=![]() ,∴PB=
,∴PB=![]() ;
;
②如图4,过E作EQ⊥CD于Q.∵DE=CE,∴DQ=![]() CD=5,∴ME=5,∴EN=MN﹣ME=5,∴AM=
CD=5,∴ME=5,∴EN=MN﹣ME=5,∴AM=![]() =5
=5![]() ,∴BN=5
,∴BN=5![]() ,同理得:
,同理得:![]() ,∴PE=PB=
,∴PE=PB=![]() ,∴PB=
,∴PB=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道1+2+3+…+
 =
= ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .[问题提出] 那么
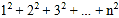 的结果等于多少呢?
的结果等于多少呢?[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+
 n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ . 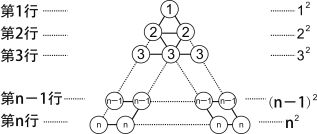
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(
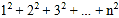 )=_________________.因此,
)=_________________.因此,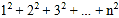 =__________.
=__________. 
图2
[问题解决]
(1).根据以上规律可得
 __________________.
__________________.(2).试计算
 ,请写出计算步骤.
,请写出计算步骤. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形
 的直角顶点
的直角顶点 在第一象限,顶点
在第一象限,顶点 、
、 分别在函数
分别在函数 图像的两个分支上,且
图像的两个分支上,且 经过原点
经过原点 ,
, 与
与 轴相交于点
轴相交于点 ,连接
,连接 ,已知
,已知 平分四边形
平分四边形 的面积.
的面积.(1)证明:
 :
:(2)求点
 的坐标.
的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)﹣10﹣(﹣16)+(﹣24);
(2)﹣3.5÷
 ×(﹣
×(﹣ )×|﹣
)×|﹣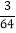 |
|(3)(
 ﹣
﹣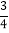 +
+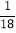 )×(﹣36)
)×(﹣36)(4)(﹣1)3+[42﹣(l﹣32)×2]
-
科目: 来源: 题型:
查看答案和解析>>【题目】
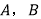 两地盛产柑桔,
两地盛产柑桔,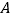 地有柑桔200吨,
地有柑桔200吨,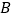 地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知
地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知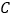 仓库可储存240吨,
仓库可储存240吨,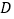 仓库可储存260吨;从
仓库可储存260吨;从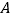 地运往C、D两处的费用分别为每吨20元和25元,从
地运往C、D两处的费用分别为每吨20元和25元,从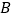 地运往C、D两处的费用分别为每吨15元和18元.设从
地运往C、D两处的费用分别为每吨15元和18元.设从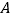 地运往
地运往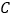 仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.(1)请填写下表后分别求出yA,yB之间的函数关系式,并写出定义域;

C
D
总计
A
x吨
200吨
B
300吨
总计
240吨
260吨
500吨
(2)试讨论A,B两地中,哪个运费较少;
-
科目: 来源: 题型:
查看答案和解析>>【题目】“国庆节大酬宾”,某商场设计的促销活动如下:在一个不透明的箱子里放有3个质地相同的小球,并在球上分别标有“5元”、“10元”和“15元”的字样,规定:在本商场同一日内,顾客每消费满300元,就可以在箱子里先后摸出两个球(第一次摸出后不放回).商场根据两个小球所标金额和返还相等价格的购物券,购物券可以在本商场消费,某顾客刚好消费300元.
(1)该顾客最多可得到元购物券;
(2)请你用画树状图和列表的方法,求出该顾客所得购物券的金额不低于25元的概率.
相关试题

