【题目】如图,等腰直角三角形![]() 的直角顶点
的直角顶点![]() 在第一象限,顶点
在第一象限,顶点![]() 、
、![]() 分别在函数
分别在函数![]() 图像的两个分支上,且
图像的两个分支上,且![]() 经过原点
经过原点![]() ,
,![]() 与
与![]() 轴相交于点
轴相交于点![]() ,连接
,连接![]() ,已知
,已知![]() 平分四边形
平分四边形![]() 的面积.
的面积.
(1)证明:![]() :
:
(2)求点![]() 的坐标.
的坐标.

参考答案:
【答案】(1)见解析 (2) A(-2,4)
【解析】(1)根据反比例函数图象的对称性和三角线的面积公式得到S△ABD=2S△ACD.即BD=2CD;
(2)如图,过点B作BE⊥x轴于E,过点C作CF⊥x于F,连接OC,构建全等三角形△OBE≌△COF,结合该全等三角形的对应边相等得到:BE=OF,OE=CF,由![]() =
=![]() =2推知BE=2OE.设OE=a,则BE=2a,所以B(a,﹣2a),根据反比例函数图象上点的坐标特征和反比例函数图象的对称性来求点A的坐标即可.
=2推知BE=2OE.设OE=a,则BE=2a,所以B(a,﹣2a),根据反比例函数图象上点的坐标特征和反比例函数图象的对称性来求点A的坐标即可.
(1)∵函数y=﹣![]() 图象关于原点对称,∴OA=OB,∴S△AOD=S△BOD.
图象关于原点对称,∴OA=OB,∴S△AOD=S△BOD.
∵AD平分四边形AODC的面积,∴S△AOD=S△ACD,∴S△ABD=2S△ACD,∴BD=2CD;
(2)如图,过点B作BE⊥x轴于E,过点C作CF⊥x于F,连接OC,则∠BEO=∠OFC=90°.
∵△ABC是等腰直角三角形,OA=OB,∴∠BOC=90°,OC=![]() AB=OB,∴∠BOE+∠COF=90°,而∠BOE+∠OBE=90°,∴∠OBE=∠COF.
AB=OB,∴∠BOE+∠COF=90°,而∠BOE+∠OBE=90°,∴∠OBE=∠COF.
∵在△OBE与△COF中, ,∴△OBE≌△COF(AAS),∴BE=OF,OE=CF.
,∴△OBE≌△COF(AAS),∴BE=OF,OE=CF.
∵∠OBE=∠COF,∴cos∠OBE=cos∠COF,∴![]() =
=![]() .
.
∵![]() =
=![]() =2,∴BE=2CF,∴BE=2OE.
=2,∴BE=2CF,∴BE=2OE.
设OE=a,则BE=2a,∴B(a,﹣2a),∴a(﹣2a)=﹣8,解得:a=2,∴B(2,﹣4),∴A(﹣2,4).

-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
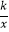 与一次函数y=kx﹣k+2在同一直角坐标系中的图象可能是( )
与一次函数y=kx﹣k+2在同一直角坐标系中的图象可能是( )
A.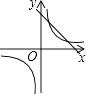
B.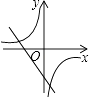
C.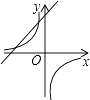
D.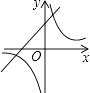
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们知道1+2+3+…+
 =
= ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .[问题提出] 那么
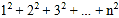 的结果等于多少呢?
的结果等于多少呢?[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+
 n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ . 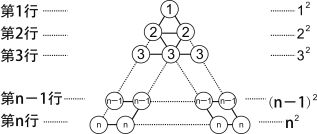
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(
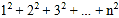 )=_________________.因此,
)=_________________.因此,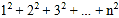 =__________.
=__________. 
图2
[问题解决]
(1).根据以上规律可得
 __________________.
__________________.(2).试计算
 ,请写出计算步骤.
,请写出计算步骤. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值. -
科目: 来源: 题型:
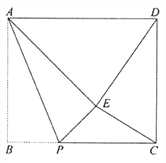
查看答案和解析>>【题目】如图,在矩形
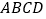 纸片中,
纸片中,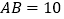 cm,
cm, cm。点
cm。点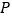 在
在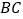 边上,将
边上,将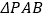 沿
沿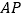 折叠,得
折叠,得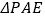 ,连接
,连接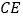 ,
, 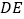 .
.(1)当点
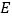 落在
落在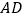 边上时,
边上时,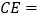 ;
;(2)当点
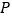 是
是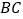 的中点时,求
的中点时,求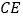 的长;
的长;(3)当
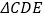 分别满足下列条件时,求相应的
分别满足下列条件时,求相应的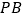 的长:
的长:①
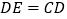 ;②
;② .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算题
(1)﹣10﹣(﹣16)+(﹣24);
(2)﹣3.5÷
 ×(﹣
×(﹣ )×|﹣
)×|﹣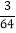 |
|(3)(
 ﹣
﹣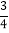 +
+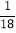 )×(﹣36)
)×(﹣36)(4)(﹣1)3+[42﹣(l﹣32)×2]
-
科目: 来源: 题型:
查看答案和解析>>【题目】
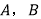 两地盛产柑桔,
两地盛产柑桔,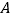 地有柑桔200吨,
地有柑桔200吨,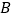 地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知
地有柑桔300吨.现将这些柑桔运到C、D两个冷藏仓库,已知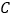 仓库可储存240吨,
仓库可储存240吨,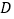 仓库可储存260吨;从
仓库可储存260吨;从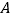 地运往C、D两处的费用分别为每吨20元和25元,从
地运往C、D两处的费用分别为每吨20元和25元,从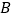 地运往C、D两处的费用分别为每吨15元和18元.设从
地运往C、D两处的费用分别为每吨15元和18元.设从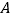 地运往
地运往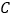 仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.
仓库的柑桔重量为x吨,A、B两地运往两仓库的柑桔运输费用分别为yA元和yB元.(1)请填写下表后分别求出yA,yB之间的函数关系式,并写出定义域;

C
D
总计
A
x吨
200吨
B
300吨
总计
240吨
260吨
500吨
(2)试讨论A,B两地中,哪个运费较少;
相关试题

