【题目】我们知道1+2+3+…+![]() =
=![]() ,则1+2+3+…+10= ___________ .
,则1+2+3+…+10= ___________ .
[问题提出] 那么 ![]() 的结果等于多少呢?
的结果等于多少呢?
[阅读理解] 在图1所示的三角形数阵中,第1行圆圈中的数为1,即12 ;第2行两个圆圈中数的和为2+2,即22;......;第n行n个圆圈中数的和为n+n+![]() n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
n即 n2;这样,该三角形数阵中共有____ 个圆圈,所有圆圈中数的和可表示为_________________ .
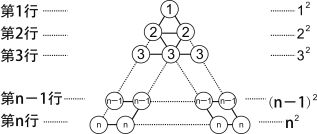
图1
[规律探究] 将三角形数阵经两次旋转可得如图2所示的三角形数阵,观察这三个三角形数阵各行同一位置圆圈中的数(如第n-1行的第一个圆圈中的数分别为n-1,2,n)发现每个位置上三个圆圈中的数的和均为______________.由此可得,这三个三角形数阵所有圆圈中数的总和为:
3(![]() )=_________________.因此,
)=_________________.因此,![]() =__________.
=__________.

图2
[问题解决]
(1).根据以上规律可得![]() __________________.
__________________.
(2).试计算 ![]() ,请写出计算步骤.
,请写出计算步骤.
参考答案:
【答案】55;![]() ;
;![]() ;(
;(![]() );
);![]() ;
;![]() ;(1)7;(2)2485
;(1)7;(2)2485
【解析】
把n=10代入1+2+3+…+![]() =
=![]() ,即可求出1+2+3+…+10的值;
,即可求出1+2+3+…+10的值;
[阅读理解]:由图1可知,共有1+2+3+…+n=![]() 个圆圈,所有圆圈中数的和可表示为
个圆圈,所有圆圈中数的和可表示为![]() ;
;
[规律探究]:由图2知,每个位置上三个圆圈中的数的和均为![]() .由此可得,这三个三角形数阵所有圆圈中数的总和为:3(
.由此可得,这三个三角形数阵所有圆圈中数的总和为:3(![]() )=每个位置上三个圆圈中的数的和(
)=每个位置上三个圆圈中的数的和(![]() )×位置的个数
)×位置的个数![]() ,因此,
,因此,![]() =
=![]() ;
;
[问题解决]:(1)先化简把![]() ,然后把n=10代入就算即可;(2)用(
,然后把n=10代入就算即可;(2)用(![]() )减去(
)减去(![]() )即可求出结论.
)即可求出结论.
当n=10时,
1+2+3+…+![]() =
=![]() =55;
=55;
[阅读理解]:由图1可知,共有1+2+3+…+n=![]() 个圆圈,所有圆圈中数的和可表示为
个圆圈,所有圆圈中数的和可表示为![]() ;
;
[规律探究]:由图2知,每个位置上三个圆圈中的数的和均为![]() .由此可得,这三个三角形数阵所有圆圈中数的总和为:3(
.由此可得,这三个三角形数阵所有圆圈中数的总和为:3(![]() )=
)=![]() ,因此,
,因此,![]() =
=![]() ;
;
[问题解决]:(1)∵![]() ,
,
把n=10代入得,
原式=![]() =7;
=7;
(2)![]()
=(![]() )-(
)-(![]() )
)
=![]()
=![]()
=2485.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个自然数的立方,可以分裂成若干个连续奇数的和,例如:23,33和43分别可以按如图所示的方式“分裂”,则63“分裂”出的奇数中,最大的奇数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】反比例函数y=
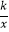 与一次函数y=kx﹣k+2在同一直角坐标系中的图象可能是( )
与一次函数y=kx﹣k+2在同一直角坐标系中的图象可能是( )
A.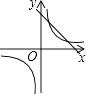
B.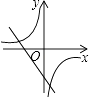
C.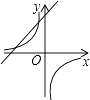
D.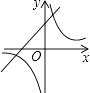
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的一元二次方程x2﹣(2k+1)x+k2+k=0.
(1)求证:方程有两个不相等的实数根;
(2)若△ABC的两边AB,AC的长是这个方程的两个实数根.第三边BC的长为5,当△ABC是等腰三角形时,求k的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等腰直角三角形
 的直角顶点
的直角顶点 在第一象限,顶点
在第一象限,顶点 、
、 分别在函数
分别在函数 图像的两个分支上,且
图像的两个分支上,且 经过原点
经过原点 ,
, 与
与 轴相交于点
轴相交于点 ,连接
,连接 ,已知
,已知 平分四边形
平分四边形 的面积.
的面积.(1)证明:
 :
:(2)求点
 的坐标.
的坐标.
-
科目: 来源: 题型:
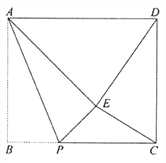
查看答案和解析>>【题目】如图,在矩形
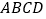 纸片中,
纸片中,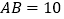 cm,
cm, cm。点
cm。点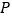 在
在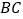 边上,将
边上,将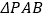 沿
沿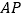 折叠,得
折叠,得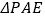 ,连接
,连接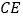 ,
, 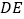 .
.(1)当点
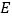 落在
落在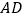 边上时,
边上时,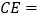 ;
;(2)当点
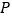 是
是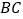 的中点时,求
的中点时,求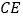 的长;
的长;(3)当
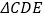 分别满足下列条件时,求相应的
分别满足下列条件时,求相应的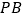 的长:
的长:①
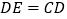 ;②
;② .
.
相关试题

