【题目】如图,矩形![]() ,点
,点![]() 、
、![]() 分别在
分别在![]() 轴、
轴、![]() 轴上, 点
轴上, 点![]() 坐标为
坐标为![]() , 连接
, 连接![]() ,将矩形
,将矩形![]() 沿
沿![]() 折叠,点
折叠,点![]() 的对应点为点
的对应点为点![]() ,则点
,则点![]() 的坐标为_____(用含
的坐标为_____(用含![]() 的式子表示).
的式子表示).
参考答案:
【答案】![]()
【解析】
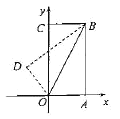
过点D做DE⊥x轴,垂足为E,交BC延长线于点F.证明△OED∽△DFB,相似比为1:2,设DE=m,表示各线段关系,求出m,进而求出点![]() 的坐标.
的坐标.
解:如图,过点D做DE⊥x轴,垂足为E,交BC延长线于点F.
∵矩形![]() 中,点
中,点![]() 坐标为
坐标为![]() ,
,
∴OA=k,AB=2k.
∵矩形![]() 沿
沿![]() 折叠,
折叠,
∴△OBD≌△OBA,
∴OD= OA=k,BD=BA=2k,∠ODB=∠OAB=90°,
∴∠FDB+∠EDO=90°.
∵∠EOD+∠EDO=90°,
∴∠EOD=∠FDB.
∵∠F=∠DEO=90°,
∴△OED∽△DFB,
∴![]() .
.
设DE=m,则BF=2m,OE=2m-k,
∴2k-m=2(2m-k)
∴![]() ,
,
∴![]()
∴点D坐标为:![]() .
.
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一副含
 和
和  角的三角板
角的三角板  和
和  叠合在一起,边
叠合在一起,边  与
与  重合,
重合,  (如图1),点
(如图1),点  为边
为边 
 的中点,边
的中点,边  与
与  相交于点
相交于点  ,此时线段
,此时线段  的长是 . 现将三角板
的长是 . 现将三角板  绕点
绕点  按顺时针方向旋转(如图2),在
按顺时针方向旋转(如图2),在  从
从  到
到  的变化过程中,点
的变化过程中,点  相应移动的路径长共为 . (结果保留根号)
相应移动的路径长共为 . (结果保留根号)
-
科目: 来源: 题型:
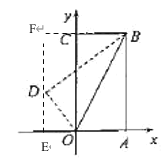
查看答案和解析>>【题目】如图,在平面直角坐标系中,直线AB分别交x、y轴于点A、B,直线BC分别交x、y轴于点C、B,点A的坐标为(3,0),∠ABO=30°,且AB⊥BC.
(1)求直线BC和AB的解析式;
(2)将点B沿某条直线折叠到点O,折痕分别交BC、BA于点E、D,在x轴上是否存在点F,使得点D、E、F为顶点的三角形是以DE为斜边的直角三角形?若存在,请求出F点坐标;若不存在,请说明理由;
(3)在平面直角坐标系内是否存在两个点,使得这两个点与B、C两点构成的四边形是正方形?若存在,请求出这两点的坐标;若不存在,请说明理由.

-
科目: 来源: 题型:
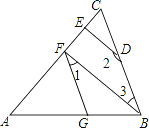
查看答案和解析>>【题目】如图,∠AGF=∠ABC,∠1+∠2=180°.
(1)试判断BF与DE的位置关系,并说明理由;
(2)若BF⊥AC,∠2=150°,求∠AFG的度数.
-
科目: 来源: 题型:
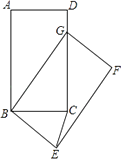
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=5,BC=3,将矩形ABCD绕点B按顺时针方向旋转得到矩形GBEF,点A落在矩形ABCD的边CD上,连接CE,则CE的长是 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形ABCD中,AD=2
 ,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 .
,把边BC绕点B逆时针旋转30°得到线段BP,连接AP并延长交CD于点E,连接PC,则三角形PCE的面积为 . 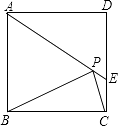
-
科目: 来源: 题型:
查看答案和解析>>【题目】两个全等的三角尺重叠放在△ACB的位置,将其中一个三角尺绕着点C按逆时针方向旋转至△DCE的位置,使点A恰好落在边DE上,AB与CE相交于点F.已知∠ACB=∠DCE=90°,∠B=30°,AB=8cm,则CF=cm.

相关试题

