【题目】下图是一座抛物线形拱桥,P 处有一照明灯,水面OA 宽4 m.从O,A 两处观测P 处,仰角分别为α,β,且tanα=![]() ,tanβ=
,tanβ=![]() .以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.
.以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.
(1)求点P的坐标;
(2)若水面上升1 m,则水面宽多少米(![]() 取1.41,结果精确到0.1 m)?
取1.41,结果精确到0.1 m)?

参考答案:
【答案】(1)点P 的坐标为(3,![]() );(2)水面上升1 m,则水面宽约2.8 m.
);(2)水面上升1 m,则水面宽约2.8 m.
【解析】
(1)过点P作PH⊥OA于H,如图,设PH=3x,运用三角函数可得OH=6x,AH=2x,根据条件OA=4可求出x,即可得到点P的坐标;
(2)若水面上升1m后到达BC位置,如图,运用待定系数法可求出抛物线的解析式,然后求出y=1时x的值,就可解决问题.
(1)如图,过点P 作PB⊥OA,垂足为B.设点P 的坐标为(x,y).在Rt△POB 中,
∵tanα=![]() ,
,
∴ OB=![]() =2y.
=2y.
在Rt△PAB 中,∵tanβ=![]() ,
,
∴ AB=![]() y.
y.
∵ OA=OB+AB,
即2y+![]() y=4,
y=4,
∴ y=![]() .
.
∴ x=2×![]() =3.
=3.
∴ 点P 的坐标为(3,![]() ).
).

(2)设这条抛物线表示的二次函数的表达式为y=ax2+bx,由函数图象经过(4,0),(3,![]() )两点,可得
)两点,可得 解方程组,得
解方程组,得 ,
,
∴这条抛物线表示的二次函数的表达式为y=-![]() x2+2x.当水面上升1 m 时,水面的纵坐标为1,即-
x2+2x.当水面上升1 m 时,水面的纵坐标为1,即-![]() x2+2x=1,解得x1=2-
x2+2x=1,解得x1=2-![]() ,x2=2+
,x2=2+![]() ,
,
∴x2-x1=2+![]() -(2-
-(2-![]() )=2
)=2![]() ≈2.8.
≈2.8.
因此,若水面上升1 m,则水面宽约2.8 m.
-
科目: 来源: 题型:
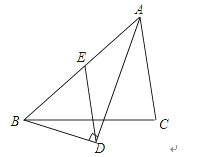
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,DE∥AC交AB于点E,若AB=8,则DE=_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(x-1)2-1.
(1)该抛物线的对称轴是______________,顶点坐标为____________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线;
x
…
…
y
…
…

(3)根据图象,直接写出当y<0时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c经过A(-1,0),B(2,0),C(0,2)三点.
(1)求这条抛物线表示的二次函数的表达式;
(2)点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,关于点
 的图象变化有以下说法:
的图象变化有以下说法:①点
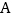 关于
关于 轴的对称点
轴的对称点 的坐标为
的坐标为
②点
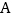 与点
与点 关于原点对称
关于原点对称③把点
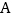 先向右平移
先向右平移 个单位长度,再向下平移
个单位长度,再向下平移 个单位长度得到点
个单位长度得到点
④把点
 绕原点顺时针旋转
绕原点顺时针旋转 ,得到点
,得到点
其中,正确的说法是( )
A. ①③④ B. ①②③④ C. ①②③ D. ②③④
相关试题

