【题目】如图,已知抛物线y=ax2+bx+c经过A(-1,0),B(2,0),C(0,2)三点.
(1)求这条抛物线表示的二次函数的表达式;
(2)点P是第一象限内此抛物线上的一个动点,当点P运动到什么位置时,四边形ABPC的面积最大?

参考答案:
【答案】(1) y=-x2+x+2;(2)当点P运动到点(1,2)的位置时,四边形ABPC的面积最大.
【解析】
(1)设交点式y=a(x+1)(x-2),然后把C点坐标代入求出a即可得到抛物线的解析式;
(2)连结OP,如图,设P(t,-t2+t+2),根据三角形面积公式,利用四边形ABPC的面积=S△AOC+S△POC+S△OBP可表示出四边形ABPC的面积=-t2+2t+3,然后利用二次函数的性质确定P点坐标.
(1)∵抛物线y=ax2+bx+c经过点C(0,2),∴c=2.
把A(-1,0),B(2,0)代入y=ax2+bx+2,得
![]() 解得
解得![]() .
.
∴这条抛物线表示的二次函数的表达式为y=-x2+x+2.
(2)设点P的坐标为(x,-x2+x+2),四边形ABPC的面积为S.连接OP,
则S=S△AOC+S△OCP+S△OBP
=![]() ×1×2+
×1×2+![]() ×2x+
×2x+![]() ×2×(-x2+x+2)=1+x-x2+x+2
×2×(-x2+x+2)=1+x-x2+x+2
=-x2+2x+3
=-(x-1)2+4.
∵a=-1<0,
∴当x=1时,四边形ABPC的面积最大.
当x=1时,y=-x2+x+2=2,
∴点P的坐标为(1,2).
即当点P运动到点(1,2)的位置时,四边形ABPC的面积最大.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,抛物线y=ax2+bx+c与x轴交于点A(-1,0),顶点坐标(1,n)与y轴的交点在(0,2),(0,3)之间(包含端点),则下列结论:①3a+b<0;②-1≤a≤-
 ;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
;③对于任意实数m,a+b≥am2+bm总成立;④关于x的方程ax2+bx+c=n-1有两个不相等的实数根.其中结论正确的个数为( )
A. 1个 B. 2个 C. 3个 D. 4个
-
科目: 来源: 题型:
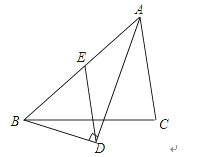
查看答案和解析>>【题目】如图,在△ABC中,AD平分∠BAC,AD⊥BD于点D,DE∥AC交AB于点E,若AB=8,则DE=_______
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知抛物线y=(x-1)2-1.
(1)该抛物线的对称轴是______________,顶点坐标为____________;
(2)选取适当的数据填入下表,并在图中的直角坐标系内描点画出该抛物线;
x
…
…
y
…
…

(3)根据图象,直接写出当y<0时,x的取值范围.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是一座抛物线形拱桥,P 处有一照明灯,水面OA 宽4 m.从O,A 两处观测P 处,仰角分别为α,β,且tanα=
 ,tanβ=
,tanβ= .以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.
.以O 为原点,OA 所在直线为x 轴建立平面直角坐标系.(1)求点P的坐标;
(2)若水面上升1 m,则水面宽多少米(
 取1.41,结果精确到0.1 m)?
取1.41,结果精确到0.1 m)?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥BC,AD⊥DC,∠BAD=100°,在BC、CD上分别找一点M、N,当△AMN的周长最小时,∠AMN+∠ANM的度数是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】化工材料经销公司购进一种化工原料若干千克,价格为每千克30元。物价部门规定其销售单价不高于每千克60元,不低于每千克30元。经市场调查发现:日销售量y(千克)是销售单价x(元)的一次函数,且当x=60时,y=80;x=50时,y=100。在销售过程中,每天还要支付其他费用450元。
(1)求出y与x的函数关系式,并写出自变量x的取值范围。
(2)求该公司销售该原料日获利w(元)与销售单价x(元)之间的函数关系式。
(3)当销售单价为多少元时,该公司日获利最大?最大获利是多少元。
相关试题

