搜索
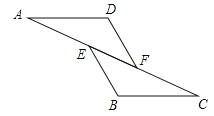
【题目】如图，已知
，
．
（1）若添加条件
，则
吗？请说明理由；
（2）若运用“
”判定
与
全等，则需添加条件：_________；
（3）若运用“
”判定与全等，则需添加条件：___________．
参考答案：
【答案】（1）
，见解析；（2）
；（3）
【解析】
(1)添加条件
，只要再推导出AF=BE，便可利用“AAS”证明出
，即可得；
(2)要利用“
”判定
与
全等，已经有了
，
。可以得到AF=BE，只要再找到图形中以AF、BE为边另外一组角相等即可；
(3)要运用“
”判定与全等，已知条件中已经有了，，即一边一角的条件，由“”的特点，再找到
，
的另外一边相等即可．
解：（1）.
理由如下：因为，所以
，即
.
在和中，因为，，.
所以
，
所以
.（全等三角形的对应边相等）.
（2）；
（3）.
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知□ABCD中，A（1，3）, B（2，-1）, C（5，-5）
（1）D的坐标为____________.
（2）若经过原点的一条直线平分□ABCD的面积，求此直线的解析式
-
科目： 来源： 题型：
查看答案和解析>>【题目】两辆汽车沿同一条路赶赴距离
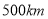的某景区．甲匀速行驶一段时间出现故障，停车检修后继续行驶．图中折线
、线段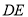
分别表示甲、乙两车所行的路程
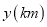与甲车出发时间
之间的关系，则下列结论中正确的个数是（ ）①甲车比乙车早出发2小时；②图中的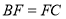
；③两车相遇时距离目的地
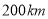；④乙车的平均速度是
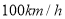；⑤甲车检修后的平均速度是
．
A.1B.2C.3D.4
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，网格线是由边长为1的小正方形格子组成的，小正方形的顶点叫做格点，以格点为顶点的多边形叫做格点多边形．小明与数学小组的同学研究发现，内部含有3个格点的四边形的面积与该四边形边上的格点数有某种关系，请你观察图中的4个格点四边形．设内部含有3个格点的四边形的面积为
，其各边上格点的个数之和为
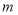，则与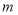之间的关系式为__________．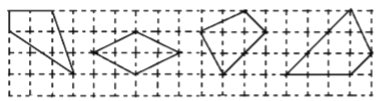
-
科目： 来源： 题型：
查看答案和解析>>【题目】小明同学在学习整式时发现，如果合理地使用乘法公式可以简化运算，于是在解此道计算题时他是这样做的（如下）：
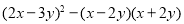
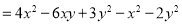第一步
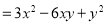第二步小华看到小明的做法后，对他说：“你做错了，在第一步运用公式时出现了错误，你好好检查一下．”小明认真仔细检查后，自己发现了一处错误圈画了出来，并进行了纠正（如下）：
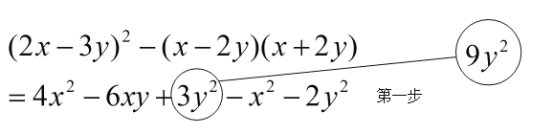
小华看到小明的改错后说：“你还有错没有改出来．”
（1）你认为小华说的对吗？_________（填“对”或“不对”）；
（2）如果小华说的对，那么小明还有哪些错误没有找出来，请你帮助小明把第一步中的其它错误圈画出来并改正，然后写出此题的正确解题过程．
-
科目： 来源： 题型：
查看答案和解析>>【题目】我市某乡镇在“精准扶贫”活动中销售一农产品，经分析发现月销售量y（万件）与月份x（月）的关系为：
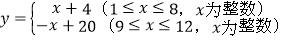，每件产品的利润z（元）与月份x（月）的关系如下表：x
1
2
3
4
5
6
7
8
9
10
11
12
z
19
18
17
16
15
14
13
12
11
10
10
10
（1）请你根据表格求出每件产品利润z（元）与月份x（月）的关系式；
（2）若月利润w（万元）=当月销售量y（万件）×当月每件产品的利润z（元），求月利润w（万元）与月份x（月）的关系式；
（3）当x为何值时，月利润w有最大值，最大值为多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】规定：如果两个一次函数的一次项系数和常数项互换，即y=kx+b和y=bx+k（其中|k|≠|b|），称这样的两个一次函数为互助一次函数，例如
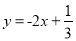和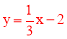
就是互助一次函数．根据规定解答下列问题：（1）填空：一次函数
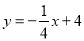与它的互助一次函数的交点坐标为______（2）若两个一次函数y=（k-b）x – k - 2b与
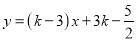是互助一次函数，求两函数图象与y轴围成的三角形的面积．
相关试题
