搜索
【题目】如图，在△ABC和△ADE中，AB=AD，AC=AE，∠1=∠2
（1）求证：△ABC≌△ADE；
（2）找出图中与∠1、∠2相等的角（直接写出结论，不需证明）．
参考答案：
【答案】（1）证明见解析;（2）∠MFD和∠NFC,理由见解析.
【解析】
（1）根据等式性质可以得出∠BAC=∠DAE，进而运用SAS判定△ABC≌△ADE； （2）根据全等三角形的对应角相等，可以发现∠B=∠D，∠E=∠C，进而得出与∠1、∠2相等的角有∠MFD和∠NFC．
本题解析：
（1）证明：∵∠1=∠2，
∴∠1+∠MAC=∠2+∠NAC，
∴∠BAC=∠DAE，
在△ABC和△ADE中，
，
∴△ABC≌△ADE（SAS）；
（2）图中与∠1、∠2相等的角有∠MFD和∠NFC．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某车间的甲、乙两名工人分别同时生产同种零件，他们一天生产零件y（个）与生产时间t（小时）的函数关系如图所示．
（1）根据图象填空：甲、乙中，______先完成一天的生产任务；在生产过程中，______因机器故障停止生产______小时．
（2）谁在哪一段时间内的生产速度最快？求该段时间内，他每小时生产零件的个数．
-
科目： 来源： 题型：
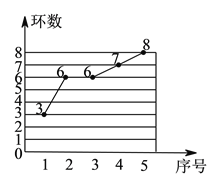
查看答案和解析>>【题目】教练想从甲、乙两名运动员中选拔一人参加射击锦标赛，故先在射击队举行了一场选拔比赛．在相同的条件下各射靶
次，每次射靶的成绩情况如图所示．甲射靶成绩的条形统计图
乙射靶成绩的折线统计图
（
）请你根据图中的数据填写下表：平均数
众数
方差
甲
__________
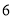
乙
__________
__________
（
）根据选拔赛结果，教练选择了甲运动员参加射击锦标赛，请给出解释． -
科目： 来源： 题型：
查看答案和解析>>【题目】实际问题
某批发商以
元/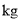 
的成本价购入了某产品
，据市场预测，该产品的销售价
（元/ 
）与保存时间
（天）的函数关系为
，但保存这批产品平均每天将损耗
．另外，批发商每天保存该批产品的费用为
元．已知该产品每天的销量不超过
，若批发商希望通过这批产品卖出获利
元，则批发商应在保存该产品多少天时一次性卖出？小明的思路及解答
本题的相等关系是：
销售价
销量
成本价
销量
保存费用
获利．解：设批发商应在保存该产品
天时一次性卖出可获利
元．根据上面的相等关系，
得
．解这个方程，得
， 
．当
时， 
（不合题意，舍去），当
时，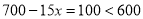 
．答：批发商应在保存该产品
天时一次性卖出可获利
元．数学老师的批改
数学老师在小明的解答中画了一条横线，并打了一个“
”．你的观点及做法
（
）请指出小明错误的原因．（
）重新给出正确的解答过程． -
科目： 来源： 题型：
查看答案和解析>>【题目】如图①，已知
是⊙
的直径， 
是
上的一个动点（点
与点
、
不重合），连接
． 
是
的中点，作弦
，垂足为
．（
）若点
和点
不重合，连接
、
和
．当
是等腰三角形时，求
的度数．（
）若点
和点
重合，如图②．探索
与
的数量关系并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某商店销售甲、乙两种商品，现有如下信息：
请结合以上信息，解答下列问题：
（1）求甲、乙两种商品的进货单价；
（2）已知甲、乙两种商品的零售单价分别为2元、3元，该商店平均每天卖出甲商品500件和乙商品1300件，经市场调查发现，甲种商品零售单价每降0.1元，甲种商品每天可多销售100件，商店决定把甲种商品的零售单价下降m（m＞0）元，在不考虑其他因素的条件下，求当m为何值时，商店每天销售甲、乙两种商品获取的总利润为1800元（注：单件利润=零售单价﹣进货单价）
-
科目： 来源： 题型：
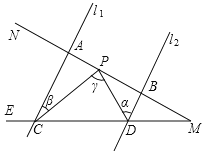
查看答案和解析>>【题目】如图，已知l1∥l2，射线MN分别和直线l1，l2交于A、B，射线ME分别和直线l1，l2交于C、D，点P在A、B间运动（P与A、B两点不重合），设∠PDB=α，∠PCA=β，∠CPD=γ．
（1）试探索α，β，γ之间有何数量关系？说明理由．
（2）如果BD=3，AB=9，AC=6，并且AC垂直于MN，那么点P运动到什么位置时，△ACP≌△BPD说明理由．
（3）在（2）的条件下，当△ACP≌△BPD时，PC与PD之间有何位置关系，说明理由．
相关试题
