【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
参考答案:
【答案】(1)36;(2)10800.
【解析】试题分析:连接AC,在Rt△ABC中根据勾股定理可求得AC的长,再由勾股定理的逆定理判定△ACD为直角三角形,根据S四边形ABCD=S△BAC+S△DAC即可求得空地ABCD的面积;(2)在(1)的基础上求解即可.
试题解析:
(1)如图,连接AC,
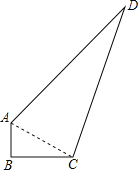
在Rt△ABC中,AC2=AB2+BC2=32+42=52,
∴AC=5m.
在△ACD中,CD2=132,AD2=122,
而122+52=132,
即AC2+AD2=CD2,
∴∠CAD=90°,
S四边形ABCD=S△BAC+S△DAC=![]() BCAB+
BCAB+![]() ADAC=
ADAC=![]() ×4×3+
×4×3+![]() ×12×5=36(m2).
×12×5=36(m2).
答:空地ABCD的面积为36m2.
(2)所以需费用为:36×300=10800(元).
答:总共需投入10800元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知Rt△ABC中,∠C=90°,AC=8.BC=6,点P以每秒1个单位的速度从
A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都
停止运动,设点P、Q运动的时间为t秒.
(Ⅰ)在运动过程中,请你用t表示P、Q两点间的距离,并求出P、Q两点间的距离
的最大值;
(Ⅱ)经过t秒的运动,求△ABC被直线PQ扫过的面积S与时间t的函数关系式.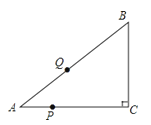
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。
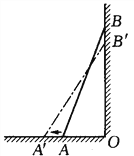
(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
-
科目: 来源: 题型:
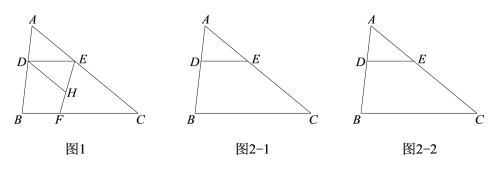
查看答案和解析>>【题目】在三角形ABC中,点D在线段AB上,DE∥BC交AC于点E,点F在直线BC上,作直线EF,过点D作直线DH∥AC交直线EF于点H.
(1)在如图1所示的情况下,求证:∠HDE=∠C;
(2)若三角形ABC不变,D,E两点的位置也不变,点F在直线BC上运动.
①当点H在三角形ABC内部时,直接写出∠DHF与∠FEC的数量关系;
②当点H在三角形ABC外部时,①中结论是否依然成立?请在图2中画图探究,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,点A,B的坐标分别为(2,m),(2,3m﹣1),若线段AB与抛物线y=x2﹣2x+2相交,则m的取值范围为
-
科目: 来源: 题型:
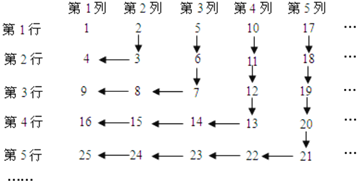
查看答案和解析>>【题目】(题文)正整数按图中的规律排列,请写出第18行,第20列的数字:_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】解方程:
(1)2x+3=x+5;
(2)2(3y-1)-3(2-4y)=9y+10;
(3)
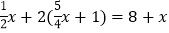
(4)
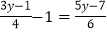 .
.
相关试题

