【题目】如图,已知Rt△ABC中,∠C=90°,AC=8.BC=6,点P以每秒1个单位的速度从
A向C运动,同时点Q以每秒2个单位的速度从A→B→C方向运动,它们到C点后都
停止运动,设点P、Q运动的时间为t秒.
(Ⅰ)在运动过程中,请你用t表示P、Q两点间的距离,并求出P、Q两点间的距离
的最大值;
(Ⅱ)经过t秒的运动,求△ABC被直线PQ扫过的面积S与时间t的函数关系式.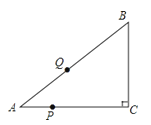
参考答案:
【答案】解:(Ⅰ)分两种情况考虑:
当Q在AB边上时,过Q作QE⊥AC,交AC于点E,连接PQ,如图1所示: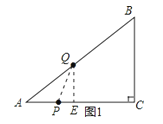
∵∠C=90°,
∴QE∥BC,
∴△ABC∽△AQE,
∴![]()
在Rt△ABC中,AC=8,BC=6,
根据勾股定理得:AB=10,
∵AQ=2t,AP=t,
∴![]() =
=![]() =
=![]() ,
,
整理得:PE=![]() t,QE=
t,QE=![]() t,
t,
根据勾股定理得:PQ2=QE2+PE2 ,
整理得:PQ=![]() t;
t;
当Q在BC边上时,连接PQ,如图2所示: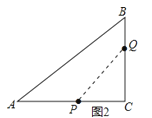
由AB+BQ=2t,AB=10,得到BQ=2t﹣10,CQ=BC﹣BQ=6﹣(2t﹣10)=16﹣2t,
由AP=t,AC=8,得到PC=8﹣t,
根据勾股定理得:PQ=![]() =
=![]() ,
,
当Q与B重合时,PQ的值最大,
则当t=5时,PQ最大值为3![]() ;
;
(Ⅱ)分两种情况考虑:
当Q在AB边上时,如图1,△ABC被直线PQ扫过的面积为S△AQP ,
此时S=![]() APQE=
APQE=![]() t
t![]() t=
t=![]() t2(0<t≤5);
t2(0<t≤5);
当Q在BC边上时,△ABC被直线PQ扫过的面积为S四边形ABQP ,
此时S=S△ABC﹣S△PQC=![]() ×8×6﹣
×8×6﹣![]() (8﹣t)(16﹣2t)=﹣t2+16t﹣40(5<t≤8).
(8﹣t)(16﹣2t)=﹣t2+16t﹣40(5<t≤8).
综上,经过t秒的运动,△ABC被直线PQ扫过的面积S与时间t的函数关系式为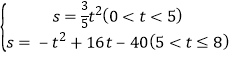 .
.
【解析】(Ⅰ)分Q在AB边上与Q在BC边上,分别如图1和图2所示,表示出PQ的长,当Q与B重合时,PQ取得最大值,求出即可;
(Ⅱ)分两种情况考虑:当Q在AB边上时,如图1,△ABC被直线PQ扫过的面积为S△AQP;当Q在BC边上时,△ABC被直线PQ扫过的面积为S四边形ABQP , 分别表示出S与t的函数关系式即可.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=8,AD=12,过点A,D两点的⊙O与BC边相切于点E,求⊙O的半径.

-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,己知O为坐标原点,点A(3,0),B(0,4),以点A为旋转中心,把△ABO顺时针旋转,得△ACD.记旋转角为α.∠ABO为β.
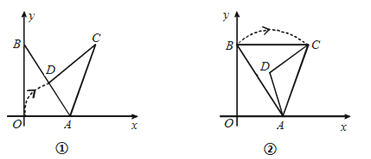
(Ⅰ)如图①,当旋转后点D恰好落在AB边上时,求点D的坐标;
(Ⅱ)如图②,当旋转后满足BC∥x轴时,求α与β之间的数量关系:
(Ⅲ)当旋转后满足∠AOD=β时,求直线CD的解析式(直接写出结果即可). -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知在△ABC中,∠B=90°,AB=8cm,BC=6cm,点P从点A开始沿△ABC的边做逆时针运动,且速度为每秒1cm;点Q从点B开始沿△ABC的边做逆时针运动,且速度为每秒2cm,他们同时出发,设运动时间为t秒.
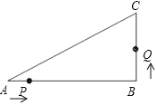
(1)出发2秒后,P,Q两点间的距离为多少cm?
(2)在运动过程中,△PQB能形成等腰三角形吗?若能,请求出几秒后第一次形成等腰三角形;若不能,则说明理由.
(3)出发几秒后,线段PQ第一次把△ABC的周长分成相等两部分?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一架梯子长25米,斜靠在一面墙上,梯子底端离墙7米。
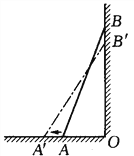
(1)这个梯子的顶端离地面有多高?
(2)如果梯子的顶端下滑了4米,那么梯子的底端在水平方向滑动了几米?
-
科目: 来源: 题型:
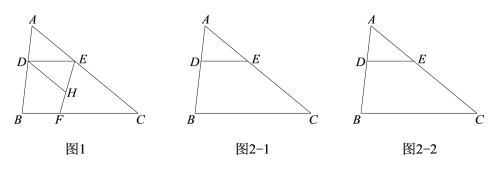
查看答案和解析>>【题目】在三角形ABC中,点D在线段AB上,DE∥BC交AC于点E,点F在直线BC上,作直线EF,过点D作直线DH∥AC交直线EF于点H.
(1)在如图1所示的情况下,求证:∠HDE=∠C;
(2)若三角形ABC不变,D,E两点的位置也不变,点F在直线BC上运动.
①当点H在三角形ABC内部时,直接写出∠DHF与∠FEC的数量关系;
②当点H在三角形ABC外部时,①中结论是否依然成立?请在图2中画图探究,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】麒麟区第七中学现有一块空地ABCD如图所示,现计划在空地上种草皮,经测量,∠B=90°,AB=3m,BC=4m,CD=13m,AD=12m.

(1)求出空地ABCD的面积?
(2)若每种植1平方米草皮需要300元,问总共需投入多少元?
相关试题

