【题目】已知:在平面直角坐标系xOy中,直线![]() 分别交x、y轴于点A、C,点B在x轴负半轴上,过点A作
分别交x、y轴于点A、C,点B在x轴负半轴上,过点A作![]() 于点K,若
于点K,若![]() ,
,![]() .
.
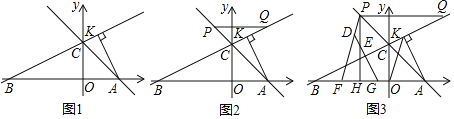
![]() 如图1,求点B坐标;
如图1,求点B坐标;
![]() 如图2,点P为AC延长线上一点,过点P作
如图2,点P为AC延长线上一点,过点P作![]() 交直线BC于点Q,设点P的横坐标为t,PQ长为d,求d与t的函数关系式
交直线BC于点Q,设点P的横坐标为t,PQ长为d,求d与t的函数关系式![]() 不必写出自变量t的取值范围
不必写出自变量t的取值范围![]() ;
;
![]() 在
在![]() 的条件下,连接OK,过点P作
的条件下,连接OK,过点P作![]() 轴于点H,点F为HB上一点,连接PF,点D在PF上,将点F沿x轴正方向平移
轴于点H,点F为HB上一点,连接PF,点D在PF上,将点F沿x轴正方向平移![]() 个单位到点G,连接DG,交PH于点E,若
个单位到点G,连接DG,交PH于点E,若![]() ,
,![]() ,
,![]() ,求点P坐标.
,求点P坐标.
参考答案:
【答案】![]() ;
;![]() ;
;![]() .
.
【解析】
(1)由三角函数求出![]() ,再求
,再求![]() ,
,![]() ,根据
,根据![]() ,可得B的坐标;(2)先求直线BC的解析式为
,可得B的坐标;(2)先求直线BC的解析式为![]() ,设
,设![]() ,把
,把![]() 代入
代入![]() 得,
得,![]() ,可得
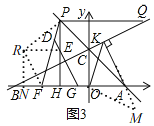
,可得![]() ;(3)如图3,过点O作
;(3)如图3,过点O作![]() 交KA延长线于点M,证
交KA延长线于点M,证![]() ≌
≌![]() ,得
,得![]() ,
,![]() ,在FN上取一点N作
,在FN上取一点N作![]() 与过点E作
与过点E作![]() 交于点R,连接PR,证矩形BHER是正方形,再证
交于点R,连接PR,证矩形BHER是正方形,再证![]() ≌
≌![]() ,
,![]() ≌
≌![]() ,求出
,求出![]() ,
,![]() ,
,![]() ,在
,在![]() 中,
中,![]() ,故
,故![]() ,求出t,再代入
,求出t,再代入![]() 中,得
中,得![]() ,所以
,所以![]() .
.
![]() ,
,
![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() ,
,
![]() 直线
直线![]() 分别交x、y轴于点A、C,
分别交x、y轴于点A、C,
![]() ,
,![]() ,
,
![]() ,
,
![]() ;
;
![]() ,
,![]() ,
,
![]() 直线BC的解析式为
直线BC的解析式为![]() ,
,
![]() 点P为AC延长线上一点,
点P为AC延长线上一点,
![]() ,
,
把![]() 代入
代入![]() 得,
得,![]() ,
,
![]() ;
;
![]() 如图3,过点O作
如图3,过点O作![]() 交KA延长线于点M,
交KA延长线于点M,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
设![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,
在FN上取一点N作![]() 与过点E作
与过点E作![]() 交于点R
交于点R
 ,
,
![]() 四边形BHER是矩形,连接PR,
四边形BHER是矩形,连接PR,
![]() ,
,
![]() ,
,
![]() 矩形BHER是正方形,
矩形BHER是正方形,
![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,![]() ,
,
![]() ≌
≌![]() ,
,
![]() ,
,
![]() ,
,
![]() ,
,![]() ,
,
在![]() 中,
中,![]() ,
,
![]() ,
,
![]() 舍
舍![]() 或
或![]() ,
,
将![]() 代入
代入![]() 中,得
中,得![]() ,
,
![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:如图,在
 中,
中,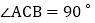 ,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且
,点D、E分别是AB、AC的中点,点F在BC延长线上,连接EF,且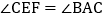 .
.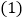 如图1,求证:四边形CDEF是平行四边形;
如图1,求证:四边形CDEF是平行四边形;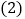 如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与
如图2,连接AF、BE,在不添加任何辅助线的情况下,请直接写出图2中所有与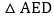 面积相等的三角形.
面积相等的三角形.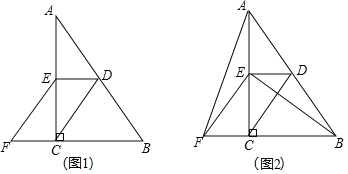
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是半圆O的直径,C是半圆O上一点,弦AD平分∠BAC,交BC于点E,若AB=6,AD=5,则DE的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知:PA是
 的切线,点B在
的切线,点B在 上,连接OB,OP,连接AB交OP于点C,
上,连接OB,OP,连接AB交OP于点C,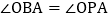 .
. 如图1,求证:
如图1,求证: ;
; 如图2,OP交
如图2,OP交 于点D,过点D作
于点D,过点D作 交AB于点E,连接OE,求证:
交AB于点E,连接OE,求证: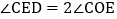 ;
; 如图3,在
如图3,在 的条件下,延长PO交
的条件下,延长PO交 于点N,连接AN交DF于点M,连接OM、EP,若
于点N,连接AN交DF于点M,连接OM、EP,若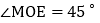 ,
, ,求线段BE的长.
,求线段BE的长.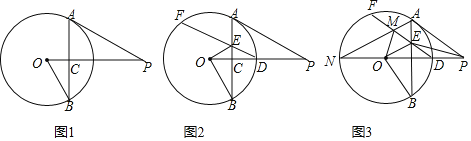
-
科目: 来源: 题型:
查看答案和解析>>【题目】某工程队修建一条长1200米的道路,采用新的施工方式,工效提升了50%,结果提前4天完成任务.
(1)求这个工程队原计划每天修建道路多少米?
(2)在这项工程中,如果要求提前2天完成任务,那么实际平均每天修建道路多少米?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠ACB=90°,BC=6,AC=8,分别以点A,B为圆心,大于线段AB长度一半的长为半径作弧,相交于点E,F,过点E,F作直线EF,交AB于点D,连结CD,则CD的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

相关试题

