【题目】如图,lA,lB分别表示A步行与B骑车在同一路上行驶的路程S与时间t的关系.
(1)B出发时与A相距______千米.
(2)B走了一段路后,自行车发生故障,进行修理,所用的时间是______小时.
(3)B出发后______小时与A相遇.
(4)若B的自行车不发生故障,保持出发时的速度前进,______小时与A相遇,相遇点离B的出发点______千米.在图中表示出这个相遇点C.
(5)求出A行走的路程S与时间t的函数关系式。

参考答案:
【答案】(1)10;(2)1;(3)3;(4)![]() ,
, ![]() ;(5)S=4t+10.
;(5)S=4t+10.
【解析】试题分析:
(1)由图可知,B出发时与A相距10km;
(2)由图可知,B修自行车所用时间为:1.5-0.5=1(小时);
(3)由图象可知,B在出发后3小时的时候与A相遇;
(4)分别求出![]() 的函数关系式和
的函数关系式和![]() 在修车前的函数关系式,由两个解析式组成方程组,解方程组,即可求得所求答案.
在修车前的函数关系式,由两个解析式组成方程组,解方程组,即可求得所求答案.
试题解析:
(1)由图和题意可得:B出发时与A相距10千米.
故答案为:10;
(2)由图和题意可得:修理自行车的时间为:1.5-05=1(小时).
故答案为:1;
(3)由图象可得:B出发3小时时和A相遇,
故答案为:3;
(4)设lA的解析式为:S1=at+b,
∵lA过点(0,10)和(3,22),
∴![]() ,
,
解得: ![]() ,
,
∴S1=4t+10,
设B修车前的关系式为:S2=kt,
∵修车前lB过(0.5,7.5)点.
∴7.5=0.5k,解得:k=15,
∴S2=15t,
由![]() ,解得:
,解得:  ,
,
即若B的自行车不发生故障,保持出发时的速度前进,则![]() 小时时相遇,此时B走的路程是
小时时相遇,此时B走的路程是![]() 千米.在图中用点C表示相遇点如下图所示:
千米.在图中用点C表示相遇点如下图所示:
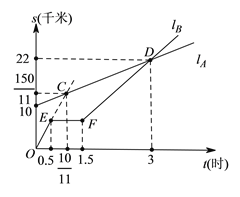
(5)由(4)得:A行走的路程S与时间t的函数关系式为:S=4t+10.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一次函数y=kx+b与y=kbx,它们在同一坐标系内的图象可能为 ( )
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,射线OA的方向是北偏东20°,射线OB的方向是北偏西40°,OD是OB的反向延长线.若OC是∠AOD的平分线,则∠BOC=_____°,射线OC的方向是_____.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB和CD的公共部分BD=
 AB=
AB=  CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
CD,线段AB、CD的中点E,F之间距离是10cm,求AB,CD的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某船向正东航行,在A处望见灯塔C在东北方向,前进到B处望见灯塔C在北偏西30°,又航行了半小时到D处,望见灯塔C恰在西北方向,若船速为每小时20海里.求A、D两点间的距离.(结果不取近似值)

-
科目: 来源: 题型:
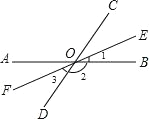
查看答案和解析>>【题目】如图,直线 AB、CD 相交于 O,∠BOC=70°,OE 是∠BOC 的角平分线,OF是OE的反向延长线.
(1)求∠1,∠2,∠3 的度数;
(2)判断 OF 是否平分∠AOD,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,方格纸上的每个小方格都是边长为1的正方形,△ABC 的顶点均在格点上,若 B
点的坐标为(-4,-2), 按要求回答下列问题:
(1)在图中建立正确的平面直角坐标系;
(2)根据所建立的坐标系,写出点A和点C的坐标;
(3)画出△ABC关于x轴的对称图形△ABC;
(4)△ABC 的面积为________.

相关试题

