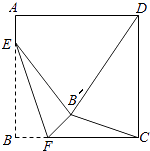
【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为 . 
参考答案:
【答案】16或4 ![]()
【解析】解:(i)当B′D=B′C时,
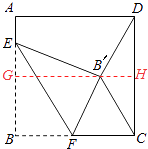
过B′点作GH∥AD,则∠B′GE=90°,
当B′C=B′D时,AG=DH= ![]() DC=8,
DC=8,
由AE=3,AB=16,得BE=13.
由翻折的性质,得B′E=BE=13.
∴EG=AG﹣AE=8﹣3=5,
∴B′G= ![]() =
= ![]() =12,
=12,
∴B′H=GH﹣B′G=16﹣12=4,
∴DB′= ![]() =
= ![]() =4
=4 ![]()
(ii)当DB′=CD时,则DB′=16(易知点F在BC上且不与点C、B重合).
(iii)当CB′=CD时,
∵EB=EB′,CB=CB′,
∴点E、C在BB′的垂直平分线上,
∴EC垂直平分BB′,
由折叠可知点F与点C重合,不符合题意,舍去.
综上所述,DB′的长为16或4 ![]() .
.
故答案为:16或4 ![]() .
.
根据翻折的性质,可得B′E的长,根据勾股定理,可得CE的长,根据等腰三角形的判定,可得答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
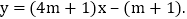
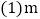 为何值时,y随x的增大而减小?
为何值时,y随x的增大而减小? 为何值时,直线与y轴的交点在x轴下方?
为何值时,直线与y轴的交点在x轴下方?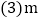 为何值时,直线位于第二、三、四象限?
为何值时,直线位于第二、三、四象限? -
科目: 来源: 题型:
查看答案和解析>>【题目】夏季来临,商场准备购进甲、乙两种空调
 已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同
已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同 请解答下列问题:
请解答下列问题: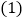 求甲、乙两种空调每台的进价;
求甲、乙两种空调每台的进价;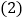 若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润
若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润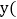 元
元 与甲种空调
与甲种空调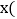 台
台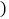 之间的函数关系式;
之间的函数关系式; 在
在 的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元
的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元 台的A型按摩器和700元
台的A型按摩器和700元 台的B型按摩器
台的B型按摩器 直接写出购买按摩器的方案.
直接写出购买按摩器的方案. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
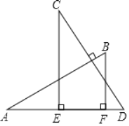
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
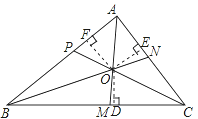
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
-
科目: 来源: 题型:
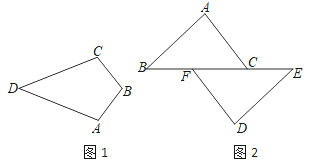
查看答案和解析>>【题目】(1)如图1,在四边形ABCD中,AB=CB,AD=CD.求证:∠C=∠A.
(2)如图2,点B、F、C、E在一条直线上,FB=CE,AB∥ED,AC∥FD.求证:AB=DE.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某蔬菜经销商去蔬菜生产基地批发某种蔬菜,已知这种蔬菜的批发量在20千克~60千克之间(含20千克和60千克)时,每千克批发价是5元;若超过60千克时,批发的这种蔬菜全部打八折,但批发总金额不得少于300元.
(1)根据题意,填写如表:蔬菜的批发量(千克)
…
25
60
75
90
…
所付的金额(元)
…
125
300
…
(2)经调查,该蔬菜经销商销售该种蔬菜的日销售量y(千克)与零售价x(元/千克)是一次函数关系,其图象如图,求出y与x之间的函数关系式;
(3)若该蔬菜经销商每日销售此种蔬菜不低于75千克,且当日零售价不变,那么零售价定为多少时,该经销商销售此种蔬菜的当日利润最大?最大利润为多少元?
相关试题

