【题目】夏季来临,商场准备购进甲、乙两种空调![]() 已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同
已知甲种空调每台进价比乙种空调多500元,用40000元购进甲种空调的数量与用30000元购进乙种空调的数量相同![]() 请解答下列问题:
请解答下列问题:
![]() 求甲、乙两种空调每台的进价;
求甲、乙两种空调每台的进价;
![]() 若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润
若甲种空调每台售价2500元,乙种空调每台售价1800元,商场欲同时购进两种空调20台,且全部售出,请写出所获利润![]() 元
元![]() 与甲种空调
与甲种空调![]() 台
台![]() 之间的函数关系式;
之间的函数关系式;
![]() 在
在![]() 的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元
的条件下,若商场计划用不超过36000元购进空调,且甲种空调至少购进10台,并将所获得的最大利润全部用于为某敬老院购买1100元![]() 台的A型按摩器和700元
台的A型按摩器和700元![]() 台的B型按摩器
台的B型按摩器![]() 直接写出购买按摩器的方案.
直接写出购买按摩器的方案.
参考答案:
【答案】(1) 甲、乙两种空调每台进价分别为2000元,1500元;(2)y=200x+6000;(3)两种购买方案:A型0台,B型12台或A型7台,B型1台.
【解析】
(1)根据题意可以列出相应的方程,从而可以分别求得甲、乙两种空调每台的进价,注意分式方程要检验;
(2)根据题意和(1)中的答案可以得到所获利润y(元)与甲种空调x(台)之间的函数关系式;
(3)根据商场计划用不超过36000元购进空调共20台,可以求得x的取值范围,从而可以求得所能获得的最大利润.
![]() 设乙种空调每台进价为x元,则甲种空调每台进价为
设乙种空调每台进价为x元,则甲种空调每台进价为![]() 元,
元,
根据题意得:![]() ,
,
去分母得:![]() ,
,
解得:![]() ,
,
经检验![]() 是分式方程的解,且
是分式方程的解,且![]() ,
,
则甲、乙两种空调每台进价分别为2000元,1500元;
![]() 根据题意得:
根据题意得:![]() ;
;
![]() 设购买甲种空调n台,则购买乙种空调
设购买甲种空调n台,则购买乙种空调![]() 台,
台,
根据题意得:![]() ,且
,且![]() ,
,
解得:![]() ,
,
当![]() 时,最大利润为8400元,
时,最大利润为8400元,
设购买A型按摩器a台,购买B型按摩器b台,则![]() ,
,
有两种购买方案:![]() 型0台,B型12台;
型0台,B型12台;![]() 型7台,B型1台.
型7台,B型1台.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据题意解答
(1)如图1,在四边形ABCD中,AB=AD,∠BAD=120°,∠B=∠ADC=90°,E、F分别是BC、CD上的点,且∠EAF=60°,延长FD到点G,使DG=BE,连接AG,先证明△ABE≌△ADG,再证明△AEF≌△AGF,可得线段BE、EF、FD之间的数量关系为 .
(2)如图2,在四边形ABCD中,AB=AD,∠B+∠D=180°,E、F分别是BC、CD上的点,且∠EAF= ∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
∠BAD,线段BE、EF、FD之间存在什么数量关系,为什么?
(3)如图3,点A在点O的北偏西30°处,点B在点O的南偏东70°处,且AO=BO,点A沿正东方向移动249米到达E处,点B沿北偏东50°方向移动334米到达点F处,从点O观测到E、F之间的夹角为70°,根据(2)的结论求E、F之间的距离.
-
科目: 来源: 题型:
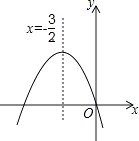
查看答案和解析>>【题目】如图,已知二次函数y=ax2+bx+c的图象如图所示,给出以下四个结论:①abc=0;②a+b+c>0;③a>b;④4ac﹣b2<0.其中正确结论有 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数
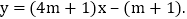
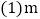 为何值时,y随x的增大而减小?
为何值时,y随x的增大而减小? 为何值时,直线与y轴的交点在x轴下方?
为何值时,直线与y轴的交点在x轴下方?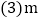 为何值时,直线位于第二、三、四象限?
为何值时,直线位于第二、三、四象限? -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥CD,且AB=CD.E、F是AD上两点,CE⊥AD,BF⊥AD.若CE=a,BF=b,EF=c,则AD的长为( )
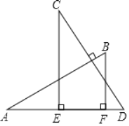
A. a+cB. b+cC. a﹣b+cD. a+b﹣c
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长是16,点E在边AB上,AE=3,点F是边BC上不与点B,C重合的一个动点,把△EBF沿EF折叠,点B落在B′处.若△CDB′恰为等腰三角形,则DB′的长为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读并理解下面的证明过程,并在每步后的括号内填写该步推理的依据.
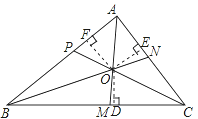
已知:如图,AM,BN,CP是△ABC的三条角平分线.
求证:AM、BN、CP交于一点.
证明:如图,设AM,BN交于点O,过点O分别作OD⊥BC,OF⊥AB,垂足分别为点D,E,F.
∵O是∠BAC角平分线AM上的一点( ),
∴OE=OF( ).
同理,OD=OF.
∴OD=OE( ).
∵CP是∠ACB的平分线( ),
∴O在CP上( ).
因此,AM,BN,CP交于一点.
相关试题

