【题目】如图,在□ABCD中,点E在AD上,以BE为折痕将△ABE翻折,点A恰好落在CD边上的点F处. 已知△EDF的周长为12,△BCF的周长为22,求CF的长.

参考答案:
【答案】FC=5.
【解析】
根据翻折变换的性质、平行四边形的性质证明AB+BC=17,此为解题的关键性结论;运用△FCB的周长为22,求出FC的长,即可解决问题.
如图,∵四边形ABCD为平行四边形,
∴AD=BC,AB=DC;
由题意得:AE=EF,AB=BF;
∵△FDE的周长为12,△FCB的周长为22,∴DE+DF+EF=12,CF+BC+BF=22,
∴(DE+EA)+(DF+CF)+BC+AB=34,即2(AB+BC)=34,
∴AB+BC=17,即BF+BC=17,
∴FC=22-17=5.
故答案为:FC=5.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(﹣1)2017﹣(﹣
 )﹣3+(cos68°﹣2)0+|4
)﹣3+(cos68°﹣2)0+|4 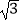 ﹣8sin60°|
﹣8sin60°| -
科目: 来源: 题型:
查看答案和解析>>【题目】四边形ABCD为矩形,G是BC上的任意一点,DE⊥AG于点E.
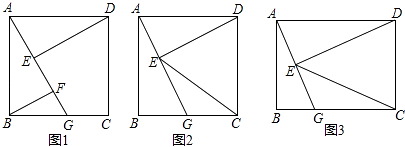
(1)如图1,若AB=BC,BF∥DE,且交AG于点F,求证:AF﹣BF=EF;
(2)如图2,在(1)条件下,AG=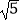 BG,求
BG,求 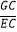 ;
;
(3)如图3,连EC,若CG=CD,DE=2,GE=1,则CE=(直接写出结果) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AB=CB,∠ABC=90°,F为AB延长线上一点,点E在BC上,且AE=CF.

(1)求证:△ABE≌△CBF;
(2)若∠CAE=30°,求∠ACF的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】早晨小欣与妈妈同时从家里出发,步行与自行车向相反方向的两地上学与上班,如图是他们离家的路程
 米
米 与时间
与时间 分钟
分钟 之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米
之间的函数图象,妈妈骑车走了10分钟时接到小欣的电话,立即以原速度返回并前往学校,若已知小欣步行的速度为50米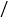 分钟,并且妈妈与小欣同时到达学校
分钟,并且妈妈与小欣同时到达学校 完成下列问题:
完成下列问题: 在坐标轴两处的括号内填入适当的数据;
在坐标轴两处的括号内填入适当的数据; 求小欣早晨上学需要的时间.
求小欣早晨上学需要的时间.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某种子商店销售“黄金一号”玉米种子,为惠民促销,推出两种销售方案供采购者选择.
方案一:每千克种子价格为4元,均不打折;
方案二:购买3千克以内(含3千克)的价格为每千克5元,若一次购买超过3千克,则超出部分的种子打七折.
(1)请分别求出方案一、方案二中购买的种子数量x(千克)与付款金额y(元)之间的函数关系式;
(2)若你去购买一定量的种子,你会怎样选择方案?说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=ax2+bx+c(a≠0)的对称轴为直线x=﹣1,且抛物线经过A(1,0),C(0,3)两点,与x轴交于点B.
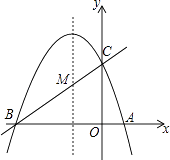
(1)若直线y=mx+n经过B、C两点,求直线BC和抛物线的解析式;
(2)在抛物线的对称轴x=﹣1上找一点M,使点M到点A的距离与到点C的距离之和最小,求出点M的坐标;
(3)设点P为抛物线的对称轴x=﹣1上的一个动点,求使△BPC为直角三角形的点P的坐标.
相关试题

