【题目】已知任意三角形的三边长,如何求三角形面积?
古希腊的几何学家海伦解决了这个问题,在他的著作《度量论》一书中给出了计算公式﹣﹣海伦公式S=![]() (其中a,b,c是三角形的三边长,p=
(其中a,b,c是三角形的三边长,p=![]() ,S为三角形的面积),并给出了证明
,S为三角形的面积),并给出了证明
例如:在△ABC中,a=3,b=4,c=5,那么它的面积可以这样计算:
∵a=3,b=4,c=5
∴p=![]() =6
=6
∴S=![]() =
=![]() =6
=6
事实上,对于已知三角形的三边长求三角形面积的问题,还可用我国南宋时期数学家秦九韶提出的秦九韶公式等方法解决.
如图,在△ABC中,BC=5,AC=6,AB=9
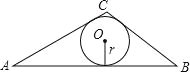
(1)用海伦公式求△ABC的面积;
(2)求△ABC的内切圆半径r.
参考答案:
【答案】(1)10![]() ;(2)r=
;(2)r=![]() .
.
【解析】
试题分析:(1)先根据BC、AC、AB的长求出P,再代入到公式S=![]() 即可求得S的值;(2)根据公式S=
即可求得S的值;(2)根据公式S=![]() r(AC+BC+AB),代入可得关于r的方程,解方程得r的值.
r(AC+BC+AB),代入可得关于r的方程,解方程得r的值.
试题解析:(1)∵BC=5,AC=6,AB=9,
∴p=![]() =
=![]() =10,
=10,
∴S=![]() =
=![]() =10
=10![]() ;
;
故△ABC的面积10![]() ;
;
(2)∵S=![]() r(AC+BC+AB),
r(AC+BC+AB),
∴10![]() =
=![]() r(5+6+9),
r(5+6+9),
解得:r=![]() ,
,
故△ABC的内切圆半径r=![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某机器零件的设计长度为1000mm,加工图纸标注尺寸为1000±0.5(mm),则合格产品的长度范围应为________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】直线y=kx+b上有两点A(x1,y1)和点B(x2,y2),且(x1-x2)(y1-y2)<0,则常数k的取值范围是_______________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】五月初,我市多地遭遇了持续强降雨的恶劣天气,造成部分地区出现严重洪涝灾害,某爱心组织紧急筹集了部分资金,计划购买甲、乙两种救灾物品共2000件送往灾区,已知每件甲种物品的价格比每件乙种物品的价格贵10元,用350元购买甲种物品的件数恰好与用300元购买乙种物品的件数相同
(1)求甲、乙两种救灾物品每件的价格各是多少元?
(2)经调查,灾区对乙种物品件数的需求量是甲种物品件数的3倍,若该爱心组织按照此需求的比例购买这2000件物品,需筹集资金多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】一张长方形桌子的长是150cm,宽是100cm,现在要设计一块长方形桌布,面积是桌面的2倍,且使四周垂下的边宽是xcm.根据题意,得( )
A. (150+x)(100+x)=150×100×2 B. (150+2x)(100+2x)=150×100×2
C. (150+x)(100+x)=150×100 D. 2(150x+100x)=150×100
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABD、△BCE、△ACF都是等边三角形。

(1)试判断四边形ADEF的形状并说明理由.
(2)当△ABC满足_____,四边形ADEF是矩形(不需证明).
(3)当△ABC满足____,四边形ADEF是菱形(不需证明).
(4)当△ABC满足 ,四边形ADEF不存在. (不需证明).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一元二次方程(x﹣2018)2+2017=0的根的情况是( )
A. 有两个相等的实数根 B. 有两个不相等的实数根 C. 只有一个实数根 D. 无实数根
相关试题

