【题目】如图,点![]() 在
在![]() 的边
的边![]() 上,点
上,点![]() 在
在![]() 内部,
内部,![]() ,
,![]() ,
,![]() .
.
给出下列结论:①![]() ;②
;②![]() ;③
;③![]() ;④
;④![]() .其中正确的有( )
.其中正确的有( )

A. 1个B. 2个C. 3个D. 4个
参考答案:
【答案】D
【解析】
①由AB=AC,AD=AE,利用等式的性质得到夹角相等,利用SAS得出△BAD≌△CAE,由全等三角形的对应边相等得到BD=CE;②由等腰直角三角形的性质得到∠ABE+∠ECB=45°,等量代换得到∠ABD+∠ECB=45°;③由∠ABD+∠ECB=45°以及∠ABC=45°得到∠ABD+∠ECB+∠ABC=90°,从而得到∠BEC=90°,即可得到BD垂直于CE;④由BD垂直于CE,在直角三角形BCE和三角形CDE中,利用勾股定理列出关系式,等量代换即可作出判断.
①∵∠DAE=∠BAC=90°,
∴∠BAC+∠BAE=∠DAE+∠BAE,即∠BAD=∠CAE,
又∵AB=AC, AD=AE,
∴△BAD≌△CAE(SAS),
∴BD=CE,故①正确;
∵△BAD≌△CAE,
∴∠ABD=∠ACE,
∵AB=AC,∠BAC=90°,
∴∠ACB=∠ABC=45°,即∠ACE+∠BCE=45°,
∴∠ABD+∠ECB=45°,故②正确;
∴∠ABD+∠ECB+∠ABC=90°,
∴∠BEC=90°,即BD⊥CE,故③正确;
∴CD2=CE2+DE2,BE2+ CE2=BC2,
即CE2=CD2-DE2,BE2=BC2-CE2,
又∵AB=AC,∠BAC=90°,AD=AE,∠DAE=90°,
∴BC2=AB2+AC2=2AB2,DE2=AD2+AE2=2AD2,
∴BE2=BC2-CE2=2AB2-(CD2-2AD2)=2(AD2+AB2)-CD2,故④正确,
∴正确的有4个,
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在直角坐标系中,点A、B的坐标分别为(1,4)和(3,0),点C是y轴上的一个动点,且A、B、C三点不在同一条直线上,当△ABC的周长最小时,点C的坐标是

A.(0,0)B.(0,1)C.(0,2)D.(0,3)
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个内角都比与它相邻的外角的3倍还多20°,则此正多边形是_____ 边形,共有_____ 条对角线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D、E,过劣弧
 (不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若⊙O的半径为r,则Rt△MBN的周长为( )
A. r B.
 r C. 2r D.
r C. 2r D.  r
r -
科目: 来源: 题型:
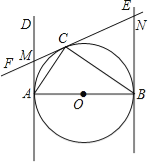
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.
(1)求证:AC∥OP;
(2)若∠APB=60°,BC=10cm,求AC的长.

相关试题

