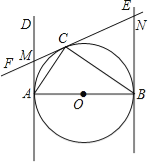
【题目】如图,已知AB为⊙O的直径,AB=2,AD和BE是圆O的两条切线,A、B为切点,过圆上一点C作⊙O的切线CF,分别交AD、BE于点M、N,连接AC、CB,若∠ABC=30°,则AM= .
参考答案:
【答案】![]() .
.
【解析】试题分析:连接OM,OC,由OB=OC,且∠ABC的度数求出∠BCO的度数,利用外角性质求出∠AOC度数,利用切线长定理得到MA=MC,利用HL得到三角形AOM与三角形COM全等,利用全等三角形对应角相等得到OM为角平分线,求出∠AOM为30°,在直角三角形AOM中,利用锐角三角函数定义即可求出AM的长.
解:连接OM,OC,
∵OB=OC,且∠ABC=30°,
∴∠BCO=∠ABC=30°,
∵∠AOC为△BOC的外角,
∴∠AOC=2∠ABC=60°,
∵MA,MC分别为圆O的切线,
∴MA=MC,且∠MAO=∠MCO=90°,
在Rt△AOM和Rt△COM中,
![]() ,
,
∴Rt△AOM≌Rt△COM(HL),
∴∠AOM=∠COM=![]() ∠AOC=30°,
∠AOC=30°,
在Rt△AOM中,OA=![]() AB=1,∠AOM=30°,
AB=1,∠AOM=30°,
∴tan30°=![]() ,即
,即![]() =
=![]() ,
,
解得:AM=![]() .
.
故答案为:![]() .
.

-
科目: 来源: 题型:
查看答案和解析>>【题目】一个正多边形的每个内角都比与它相邻的外角的3倍还多20°,则此正多边形是_____ 边形,共有_____ 条对角线.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,Rt△ABC的内切圆⊙O与两直角边AB、BC分别相切于点D、E,过劣弧
 (不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若⊙O的半径为r,则Rt△MBN的周长为( )
(不包括端点D、E)上任一点作⊙O的切线MN与AB、BC分别交于点M、N.若⊙O的半径为r,则Rt△MBN的周长为( )
A. r B.
 r C. 2r D.
r C. 2r D.  r
r -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点
 在
在 的边
的边 上,点
上,点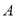 在
在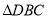 内部,
内部,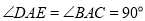 ,
, ,
,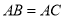 .
.给出下列结论:①
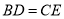 ;②
;②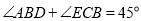 ;③
;③ ;④
;④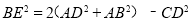 .其中正确的有( )
.其中正确的有( )
A. 1个B. 2个C. 3个D. 4个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图的七边形ABCDEFG中,AB、ED的延长线相交于O点.若图中∠1、∠2、∠3、∠4的外角的角度和为220°,则∠BOD的度数是( )

A. 400 B. 450 C. 500 D. 600
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,PA、PB分别切⊙O于A、B,BC为⊙O的直径.
(1)求证:AC∥OP;
(2)若∠APB=60°,BC=10cm,求AC的长.

-
科目: 来源: 题型:
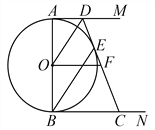
查看答案和解析>>【题目】如图,AB是⊙O的直径,AM和BN是它的两条切线,DE切⊙O于点E,交AM于点D,交BN于点C,F是CD的中点,连接OF.
(1)求证:OD∥BE;
(2)猜想:OF与CD有何数量关系?并说明理由.
相关试题

