【题目】某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价-进价)不少于750元,且甲商品的件数不能低于48件,请你帮忙求出该商场有几种进货方案?
(3)在(2)的基础上,商场预备用2500元资金来进货.若商场选择能使总利润最大的进货方案,试判断商场预备的资金是否够?
参考答案:
【答案】(1)能购进甲种商品40件,乙种商品60件;(2)有3种方案:①甲48件,乙52件;②甲49件,乙51件;③甲50件,乙50件;(3)商场预备的资金不够,理由见解析
【解析】
(1)首先设甲种商品x件,乙种商品y件,根据题意列出二元一次方程组,解得即可;
(2)首先设甲商品a件,则乙商品![]() 件,根据题意列出一元一次不等式组,解得即可得出方案;
件,根据题意列出一元一次不等式组,解得即可得出方案;
(3)根据(2)中的方案,首先计算出每种方案的总利润,选出总利润最大的方案,然后计算资金,与预备的相比较即可.
解:(1)设甲种商品x件,乙种商品y件
![]()
解得![]()
答:能购进甲种商品40件,乙种商品60件.
(2)设甲商品a件,则乙商品![]() 件
件
![]()
解得![]()
∴共有3种方案:①甲48件,乙52件;②甲49件,乙51件;③甲50件,乙50件
(3)方案①![]()
②![]()
③![]()
总利润最大的是方案①:760元
此时,![]()
![]()
∴商场预备的资金不够.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
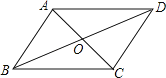
A.AB=CDB.AD∥BCC.OA=OCD.AD=BC
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,OE⊥BD交BC于点E,CD=1,则CE的长为( )
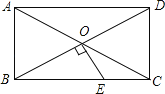
A.
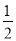 B.
B.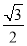 C.
C.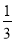 D.
D.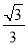
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班在甲、乙两名同学中选拔一人参加学校数学竞赛,在相同的测试条件下,两人5次测试成绩(单位:分)如下:
次数
1
2
3
4
5
甲
79
86
82
85
83
乙
88
79
90
81
77
回答下列问题:
(1)请分别求出甲、乙两同学测试成绩的平均数;
(2)经计算知
 ,
, ,你认为选拔谁参加比赛更合适,说明理由.
,你认为选拔谁参加比赛更合适,说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】某企业在“蜀南竹海”收购毛竹,直接销售,每吨可获利100元,进行粗加工,每天可加工8吨,每吨可获利800元;如果对毛竹进行精加工,每天可加工1吨,每吨可获利4000元.由于受条件限制,每天只能采用一种方式加工,要求将在一月内(30天)将这批毛竹93吨全部销售.为此企业厂长召集职工开会,让职工讨论如何加工销售更合算.
甲说:将毛竹全部进行粗加工后销售;
乙说:30天都进行精加工,未加工的毛竹直接销售;
丙说:30天中可用几天粗加工,再用几天精加工后销售;
请问厂长应采用哪位说的方案做,获利最大?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一条直线经过点A(5,0),B(1,4).
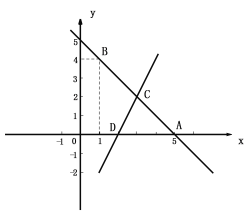
(1)求直线AB的解析式;
(2)若直线
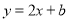 与直线AB相交于点C(3,
与直线AB相交于点C(3,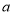 ),与
),与 轴相交于点D,求
轴相交于点D,求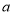 、
、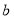 的值以及△ACD的面积.
的值以及△ACD的面积.
相关试题

