【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

参考答案:
【答案】(1)证明见解析;(2)4.9.
【解析】试题分析:(1)由正方形的性质得出AB=AD,∠B=90°,AD∥BC,得出∠AMB=∠EAF,再由∠B=∠AFE,即可得出结论;
(2)由勾股定理求出AM,得出AF,由△ABM∽△EFA得出比例式,求出AE,即可得出DE的长.
试题解析:(1)∵四边形ABCD是正方形,
∴AB=AD,∠B=90°,AD∥BC,
∴∠AMB=∠EAF,
又∵EF⊥AM,
∴∠AFE=90°,
∴∠B=∠AFE,
∴△ABM∽△EFA;
(2)∵∠B=90°,AB=12,BM=5,
∴AM=![]() =13,AD=12,
=13,AD=12,
∵F是AM的中点,
∴AF=![]() AM=6.5,
AM=6.5,
∵△ABM∽△EFA,
∴![]() ,
,
即![]() ,
,
∴AE=16.9,
∴DE=AE-AD=4.9.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列命题中,属于真命题的是( )
A.各边相等的多边形是正多边形
B.矩形的对角线互相垂直
C.三角形的中位线把三角形分成面积相等的两部分
D.对顶角相等 -
科目: 来源: 题型:
查看答案和解析>>【题目】某日孙老师佩戴运动手环进行快走锻炼,两次锻炼后数据如下表.与第一次锻炼相比,孙老师第二次锻炼步数增长的百分率是其平均步长减少的百分率的3倍.根据经验已知孙老师第二次锻炼时平均步长减少的百分率小于0.5.
项目
第一次锻炼
第二次锻炼
步数(步)
10000
①
平均步长(米/步)
0.6
②
距离(米)
6000
7020
注:步数×平均步长=距离.
(1)求孙老师第二次锻炼时平均步长减少的百分率;
(2)孙老师发现好友中步数排名第一为24000步,因此在两次锻炼结束后又走了500米,使得总步数恰好为24000步,求孙老师这500米的平均步长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两商场各自推出不同的优惠方案:在甲商场累计购物超过100元后,超出100元的部分按90%收费;在乙商场累计购物超过50元后,超出50元的部分按95%收费,设小红在同一商场累计购物x元,其中x>100.
(1)根据题意,填写下表(单位:元):
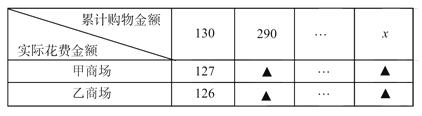
(2)当x取何值时,小红在甲、乙两商场的实际花费金额相同?
(3)请你根据小红累计购物的金额选择花费较少的商场?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC为等边三角形,AE=CD,AD,BE相交于点P,BQ⊥AD于Q,PQ=3,PE=1.
(1)求证:BE=AD;
(2)求AD的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】(1)如图①,OP是∠MON的平分线,点A为OM上一点,点B为OP上一点.请你利用该图形在ON上找一点C,使△COB≌△AOB,请在图①画出图形.参考这个作全等三角形的方法,解答下列问题:
(2)如图②,在△ABC中,∠ACB是直角,∠B=60°,AD、CE分别是∠BAC、∠BCA的平分线,AD、CE相交于点F.请你写出FE与FD之间的数量关系,并说明理由;
(3)如图③,在△ABC中,如果∠ACB不是直角,而(1)中的其他条件不变,在(2)中所得结论是否仍然成立?请你直接作出判断,不必说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,AC=6,BC=8.动点P从点A开始沿折线AC-CB-BA运动,点P在AC,CB,BA边上运动的速度分别为每秒3,4,5个单位.直线l从与AC重合的位置开始,以每秒
 个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.
个单位的速度沿CB方向移动,移动过程中保持l∥AC,且分别与CB,AB边交于E,F两点,点P与直线l同时出发,设运动的时间为t秒,当点P第一次回到点A时,点P和直线l同时停止运动.(1)当t=5秒时,点P走过的路径长为_________;当t=_________秒时,点P与点E重合;
(2)当点P在AC边上运动时,连结PE,并过点E作AB的垂线,垂足为H. 若以C、P、E为顶点的三角形与△EFH相似,试求线段EH的值;
(3)当点P在折线AC-CB-BA上运动时,作点P关于直线EF的对称点Q.在运动过程中,若形成的四边形PEQF为菱形,求t的值.

相关试题

