【题目】如图,四边形ABCD的对角线AC,BD相交于点O,且AB∥CD,添加下列条件后仍不能判断四边形ABCD是平行四边形的是( )
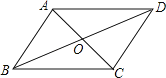
A.AB=CDB.AD∥BCC.OA=OCD.AD=BC
参考答案:
【答案】D
【解析】
根据平行四边形的判定定理逐个判断即可;
1、两组 对边分别平行的四边形是平行四边形;
2、两组对边分别相等的四边形是平行四边形;
3、对角线互相平分的四边形是平行四边形;
4、一组对边平行且相等的四边形是平行四边形;5、两组对角分别相等 的四边形是平行四边形.
A、由“一组对边平行且相等的四边形是平行四边形”可得出四边形ABCD是平行四边形;
B、由“两组对边分别平行的四边形是平行四边形”可得出四边形ABCD是平行四边形;
C、由AB∥CD可得出∠BAO=∠DCO、∠ABO=∠CDO,结合OA=OC可证出△ABO≌△CDO(AAS),根据全等三角形的性质可得出AB=CD,由“一组对边平行且相等的四边形是平行四边形”可得出四边形ABCD是平行四边形;
D、由AB∥CD、AD=BC无法证出四边形ABCD是平行四边形.
故选D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在平面直角坐标系中,
 ,
, ,且
,且 .
.(1)求点A、B的坐标;
(2)如图1,P点为y轴正半轴上一点,连接BP,若
 ,请求出P点的坐标;
,请求出P点的坐标;(3)如图2,已知
 ,若C点是x轴上一个动点,是否存在点C,使
,若C点是x轴上一个动点,是否存在点C,使 ,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.
,若存在,请直接写出所有符合条件的点C的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一个不透明的口袋中装有2个红球(记为红1、红2),1个白球、1个黑球,这些球除颜色外都相同,将球搅匀.
(1)从中任意摸出1个球,恰好摸到红球的概率是 ;
(2)先从中任意摸出一个球,再从余下的3个球中任意摸出1个球,请用画树状图或列表法求两次都摸到红球的概率.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商品的进价为每件50元,售价为每件60元,每天可卖出190件;如果每件商品的售价每上涨1元,则每天少卖10件,设每件商品的售价上涨x元,每天的销售利润为y元.
(1)求y关于x的关系式;
(2)每件商品的售价定为多少元时,每天的利润恰为1980元?
(3)每件商品的售价定为多少元时,每天可获得最大利润?最大利润是多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD中,M为BC上一点,F是AM的中点,EF⊥AM,垂足为F,交AD的延长线于点E,交DC于点N.
(1)求证:△ABM ∽△EFA;
(2)若AB=12,BM=5,求DE的长.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,ABCD的对角线AC、BD相交于点O,△AOB是等边三角形,OE⊥BD交BC于点E,CD=1,则CE的长为( )
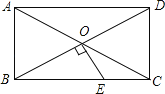
A.
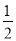 B.
B.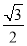 C.
C.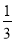 D.
D.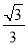
-
科目: 来源: 题型:
查看答案和解析>>【题目】某商场经销甲、乙两种商品,甲种商品每件进价15元,售价20元;乙种商品每件进价35元,售价45元.
(1)若该商场同时购进甲、乙两种商品共100件恰好用去2700元,求能购进甲、乙两种商品各多少件?
(2)该商场为使甲、乙两种商品共100件的总利润(利润=售价-进价)不少于750元,且甲商品的件数不能低于48件,请你帮忙求出该商场有几种进货方案?
(3)在(2)的基础上,商场预备用2500元资金来进货.若商场选择能使总利润最大的进货方案,试判断商场预备的资金是否够?
相关试题

