【题目】把一张矩形纸片ABC的按如图方式折叠,使顶点B落在边AD上(记为点B′),点A落在点A′处,折痕分别与边AD、BC交于点E、F. 
(1)试在图中连接BE,求证:四边形BFB′E是菱形;
(2)若AB=8,BC=16,求线段BF长能取到的整数.
参考答案:
【答案】
(1)证明:连接BB′,如图1所示:
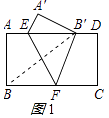
由折叠知点B、B′关于EF对称,
∴EF是线段BB′的垂直平分线,
∴BE=B′E,BF=B′F,
∵四边形ABCD是矩形,
∴AD∥BC,
∴∠B′EF=∠BFE,
由折叠得:∠B′FE=∠BFE,
∴∠B′EF=∠B′FE,
∴B′E=B′F,
∴BE=B′E=B′F=BF,
∴四边形BFB′E是菱形
(2)解:如图2所示:当点E与点A重合时,四边形ABFB′是正方形,此时BF最小,
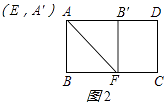
∵四边形ABFB′是正方形,
∴BF=AB=8,即BF最小为8;
如图2所示:当点B与点D重合时,BF最大,
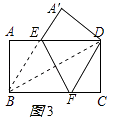
设BF=x,则CF=16﹣x,DF=BF=x,
在Rt△CDF中,由勾股定理得:CF2+CD2=DF2,
∴(16﹣x)2+82=x2,
解得:x=10,即BF=10,
∴8≤BF≤10,
∴线段BF长能取到的整数值为8,9,10.
【解析】(1)连接BB′,由折叠知点B、B′关于EF对称,得出EF是线段BB′的垂直平分线,证出BE=B′E,BF=B′F,由矩形的性质得出∠B′EF=∠BFE,由折叠得:∠B′FE=∠BFE,得出∠B′EF=∠B′FE,证出B′E=B′F,BE=B′E=B′F=BF,即可得出结论;(2)当点E与点A重合时,四边形ABFB′是正方形,此时BF最小,由正方形的性质得出BF=AB=8,得出BF最小为8; 当点B与点D重合时,BF最大,设BF=x,则CF=16﹣x,DF=BF=x,在Rt△CDF中,由勾股定理得出方程,解方程求出BF=10,得出8≤BF≤10,即可得出结果.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年1月份起调整居民用水价格,每立方米水费上涨25%,小明家去年12
月份的水费是18元,而今年5月份的水费是36元,已知小明家今年5月份的用水量比12
月份多6 m3,求该市今年居民用水的价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF.
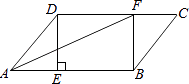
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求ABCD的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且交边CD于点E.

(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2,若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
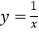 ,下列结论错误的是( )
,下列结论错误的是( )
A.图象经过点(1,1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).

(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
-
科目: 来源: 题型:
查看答案和解析>>【题目】在正方形网格中,每个小正方形的边长均为1个单位长度,△ABC的三个顶点的位置如图所示,现将△ABC平移,使点A变换为点A′,点B′、C′分别是B、C的对应点.

(1)请画出平移后的△A′B′C′,并求△A′B′C′的面积;
(2)若连接AA′,CC′,则这两条线段之间的关系是 .
相关试题

