【题目】在ABCD中,过点D作DE⊥AB于点E,点F在边CD上,DF=BE,连接AF,BF. 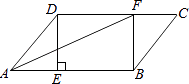
(1)求证:四边形DEBF是矩形;
(2)若AF平分∠DAB,AE=3,BF=4,求ABCD的面积.
参考答案:
【答案】
(1)证明:∵四边形ABCD是平行四边形,
∴DF∥BE,
又∵DF=BE,
∴四边形DEBF是平行四边形,
又∵DE⊥AB,
∴∠DEB=90°,
∴平行四形DEBF是矩形
(2)解:∵四边形DEBF是矩形,
∴DF∥AB,DE=BF=4,DF=BE,
∴∠DAF=∠FAB,
又∵AF平分∠DAB,
∴∠DAF=∠FAB,
∴∠DFA=∠DAF,
∴DA=DF,
又∵DE⊥AB,
∴∠DEA=90°,
在Rt△ADE中
AD= ![]() =
= ![]() =5,
=5,
∴BE=5,
∴AB=AE+BE=3+5=8,
∴ABCD的面积=ABBF=8×4=32
【解析】(1)根据平行四边形性质得出DF∥BE,得出平行四边形BFDE,根据矩形的判定得出即可;(2)根据矩形的性质求出BF=DE=4,根据勾股定理求出AD,求出AD=DF,得出AB,即可得出答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC,AB=AC=5,BC=8,∠PDQ的顶点D在BC边上,DP交AB边于点E,DQ交AB边于点O且交CA的延长线于点F(点F与点A不重合),设∠PDQ=∠B,BD=3.

(1)求证:△BDE∽△CFD;
(2)设BE=x,OA=y,求y关于x的函数关系式,并写出定义域;
(3)当△AOF是等腰三角形时,求BE的长. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在正方形网格中,每个小正方形的边长为1个单位长度.平面直角坐标系xOy的原点O在格点上,x轴、y轴都在网格线上,线段A、B在格点上.

(1)将线段AB绕点O逆时针旋转90°得到线段A1B1 , 试在图中画出线段A1B1 .
(2)在(1)的条件下,线段A2B2与线段A1B1关于原点O成中心对称,请在图中画出线段A2B2 .
(3)在(1)、(2)的条件下,点P是此平面直角坐标系内的一点,当以点A、B、B2、P为顶点的四边形为平行四边形时,请你直接写出点P的坐标: . -
科目: 来源: 题型:
查看答案和解析>>【题目】某市今年1月份起调整居民用水价格,每立方米水费上涨25%,小明家去年12
月份的水费是18元,而今年5月份的水费是36元,已知小明家今年5月份的用水量比12
月份多6 m3,求该市今年居民用水的价格.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD中,点O是对角线AC的中点,点P是线段AO上(不与A、O重合)的一个动点,过点P作PE⊥PB且交边CD于点E.

(1)求证:PB=PE;
(2)过点E作EF⊥AC于点F,如图2,若正方形ABCD的边长为2,则在点P运动的过程中,PF的长度是否发生变化?若不变,请直接写出这个不变的值;若变化,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】把一张矩形纸片ABC的按如图方式折叠,使顶点B落在边AD上(记为点B′),点A落在点A′处,折痕分别与边AD、BC交于点E、F.

(1)试在图中连接BE,求证:四边形BFB′E是菱形;
(2)若AB=8,BC=16,求线段BF长能取到的整数. -
科目: 来源: 题型:
查看答案和解析>>【题目】已知反比例函数
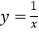 ,下列结论错误的是( )
,下列结论错误的是( )
A.图象经过点(1,1)
B.当x<0时,y随着x的增大而增大
C.当x>1时,0<y<1
D.图象在第一、三象限
相关试题

