【题目】如图,点A从原点出发沿数轴向左运动,同时,点B也从原点出发沿数轴向右运动,3秒后,两点相距15个单位长度.已知点B的速度是点A的速度的4倍(速度单位:单位长度/秒).
![]()
(1)求出点A、点B运动的速度,并在数轴上标出A、B两点从原点出发运动3秒时的位置;
(2)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动,几秒时,原点恰好处在点A、点B的正中间?
(3)若A、B两点从(1)中的位置开始,仍以原来的速度同时沿数轴向左运动时,另一点C同时从B点位置出发向A点运动,当遇到A点后,立即返回向B点运动,遇到B点后又立即返回向A点运动,如此往返,直到B点追上A点时,C点立即停止运动.若点C一直以20单位长度/秒的速度匀速运动,那么点C从开始运动到停止运动,行驶的路程是多少个单位长度?
参考答案:
【答案】(1)点A的速度为每秒1个单位长度, 点B的速度为每秒4个单位长度,图见解析;(2)运动1.8秒时,原点恰好处在A、B两点的正中间;(3)点C行驶的路程为100单位长度.
【解析】试题分析:(1)设点A的速度为每秒![]() 个单位长度,则点B的速度为每秒
个单位长度,则点B的速度为每秒![]() 个单位长度.由甲的路程+乙的路程=总路程建立方程求出其解即可;
个单位长度.由甲的路程+乙的路程=总路程建立方程求出其解即可;
设![]() 秒时,原点恰好处在点A、点B的正中间.根据两点离原点的距离相等建立方程求出其解即可;
秒时,原点恰好处在点A、点B的正中间.根据两点离原点的距离相等建立方程求出其解即可;
先根据追及问题求出A,B相遇的时间就可以求出C行驶的路程.
试题解析:(1)设点A的速度为每秒![]() 个单位长度,则点B的速度为每秒
个单位长度,则点B的速度为每秒![]() 个单位长度.依题意有:
个单位长度.依题意有: ![]() 解得
解得![]() ∴点A的速度为每秒1个单位长度,点B的速度为每秒4个单位长度.
∴点A的速度为每秒1个单位长度,点B的速度为每秒4个单位长度.
画图
![]()
(2)设![]() 秒时,原点恰好处在点A、点B的正中间.根据题意,得
秒时,原点恰好处在点A、点B的正中间.根据题意,得![]() 解得
解得![]() ,即运动1.8秒时,原点恰好处在A、B两点的正中间.
,即运动1.8秒时,原点恰好处在A、B两点的正中间.
(3)设运动![]() 秒时,点B追上点A,根据题意,得
秒时,点B追上点A,根据题意,得![]() 解得
解得![]() 即点B追上点A共用去5秒,而这个时间恰好是点C从开始运动到停止运动所花的时间,因此点C行驶的路程为:
即点B追上点A共用去5秒,而这个时间恰好是点C从开始运动到停止运动所花的时间,因此点C行驶的路程为: ![]() (单位长度)
(单位长度)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,正方形ABCD中,点A,B的坐标分别为(0,10),(8,4),点C在第一象限.动点P在正方形ABCD的边上,从点A出发沿A→B→C→D→A匀速运动,同时动点Q以相同的速度在x轴正半轴上运动,当点P到达A点时,两点同时停止运动,设运动的时间为t秒.
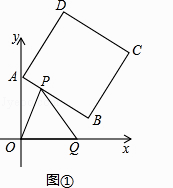
(1)当P点在边AB上运动时点Q的横坐标x(长度单位)关于运动时间t(秒)的函数图象如图②所示,请写出点Q开始运动时的坐标及点P运动速度;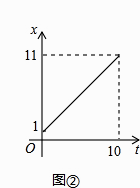
(2)求正方形边长及顶点C的坐标;
(3)在(1)中,设△OPQ的面积为S,求S与t的函数关系式并写出自变量的取值范围.
(4)如果点P、Q保持原速度不变,当点P沿A→B→C→D匀速运动时,OP与PQ能否相等?若能,写出所有符合条件的t的值;若不能,请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,将形状、大小完全相同的“
 ”和线段按照一定规律摆成下列图形.第1幅图形中“
”和线段按照一定规律摆成下列图形.第1幅图形中“ ”的个数为
”的个数为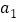 ,第2幅图形中“
,第2幅图形中“ ”的个数为
”的个数为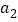 ,第3幅图形中“
,第3幅图形中“ ”的个数为
”的个数为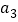 ,……,以此类推,解决以下问题:
,……,以此类推,解决以下问题:(1)直接写出
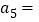 ,
,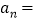 (用含n的代数式表示);
(用含n的代数式表示);(2)猜想是否存在某幅图中“
 ”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;
”的个数为2018,若存在,直接写出n的值;若不存在,则直接写出2018至少再加上多少后所得的数正好是某幅图中黑点的个数,并直接写出此时n的值;(3)求出
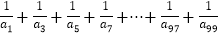 的值.
的值.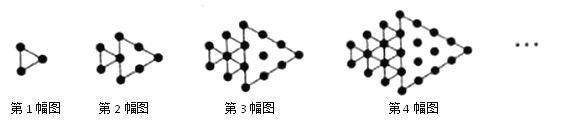
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了加强公民的节水意识,合理利用水资源,某区采用价格调控手段达到节水的目的,右下表是调控后的价目表.
(1)若该户居民8月份用水8吨,则该用户8月应交水费 元;若该户居民9月份应交水费26元,则该用户9月份用水量 吨;
(2)若该户居民10月份应交水费30元,求该用户10月份用水量;
(3)若该户居民11月、12月共用水18吨,共交水费52元,求11月、12月各应交水费多少元?

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知A=2x2+3xy﹣2x﹣1,B=﹣x2+xy﹣1:
(1)求3A+6B;
(2)若3A+6B的值与x无关,求y的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知线段AB上有两点C、D,且AC=BD,M、N分别是线段AC 、AD的中点,若AB=a cm ,AC=BD=b cm,且a,b满足(a-9)2+|b-7 |=0.

(1)求AB ,AC的长度;
(2)求线段MN的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形网格中(网格中的每个小正方形边长是1),△ABC的顶点均在格点上,请在所给的直角坐标系中解答下列问题:
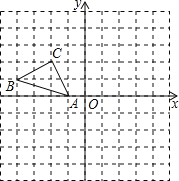
(1)作出△ABC绕点A逆时针旋转90°的△AB1C1,再作出△AB1C1关于原点O成中心对称的△A1B2C2.
(2)点B1的坐标为 ,点C2的坐标为 .
(3)△ABC经过怎样的旋转可得到△A1B2C2, .
相关试题

