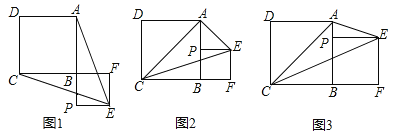
【题目】已知正方形ABCD,P为射线AB上的一点,以BP为边作正方形BPEF,使点F在线段CB的延长线上,连接EA、EC.
(1)如图1,若点P在线段AB的延长线上,求证:EA=EC;
(2)若点P在线段AB上.
①如图2,连接AC,当P为AB的中点时,判断△ACE的形状,并说明理由;
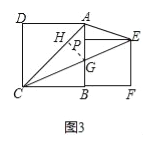
②如图3,设AB=a,BP=b,当EP平分∠AEC时,求a:b及∠AEC的度数.
参考答案:
【答案】(1)详见解析;(2)△ACE为直角三角形,理由见解析;(3)∠AEC=45°.
【解析】试题分析:(1)根据正方形的性质和全等三角形的判定定理易证△APE≌△CFE,由全等三角形的性质即可得结论;(2)①根据正方形的性质、等腰直角三角形的性质即可判定△ACE为直角三角形;②根据PE∥CF,得到![]() ,代入a、b的值计算求出a:b,根据角平分线的判定定理得到∠HCG=∠BCG,证明∠AEC=∠ACB,即可求出∠AEC的度数.
,代入a、b的值计算求出a:b,根据角平分线的判定定理得到∠HCG=∠BCG,证明∠AEC=∠ACB,即可求出∠AEC的度数.
试题解析:(1)证明:∵四边形ABCD为正方形
∴AB=AC
∵四边形BPEF为正方形
∴∠P=∠F=90°,PE=EF=FB=BP
∵AP=AB+BP,CF=BC+BF
∴CF=AP
在△APE和△CFE中:EP="EF," ∠P="∠F=90°," AP= CF
∴△APE≌△CFE
∴EA=EC
(2)①∵P为AB的中点,
∴PA=PB,又PB=PE,
∴PA=PE,
∴∠PAE=45°,又∠DAC=45°,
∴∠CAE=90°,即△ACE是直角三角形;
②∵EP平分∠AEC,EP⊥AG,
∴AP=PG=a﹣b,BG=a﹣(2a﹣2b)=2b﹣a
∵PE∥CF,
∴![]() ,即
,即![]() ,
,
解得,a=![]() b;
b;
作GH⊥AC于H,
∵∠CAB=45°,
∴HG=![]() AG=
AG=![]() ×(2
×(2![]() b﹣2b)=(2﹣
b﹣2b)=(2﹣![]() )b,又BG=2b﹣a=(2﹣
)b,又BG=2b﹣a=(2﹣![]() )b,
)b,
∴GH=GB,GH⊥AC,GB⊥BC,
∴∠HCG=∠BCG,
∵PE∥CF,
∴∠PEG=∠BCG,
∴∠AEC=∠ACB=45°.
∴a:b=![]() :1;∴∠AEC=45°.
:1;∴∠AEC=45°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】根据已知条件作符合条件的三角形,在作图过程中主要依据是( )
A. 用尺规作一条线段等于已知线段; B. 用尺规作一个角等于已知角
C. 用尺规作一条线段等于已知线段和作一个角等于已知角; D. 不能确定
-
科目: 来源: 题型:
查看答案和解析>>【题目】完成下面推理过程:
如图,已知∠1=∠2,∠B=∠C,可推得AB∥CD.理由如下:

∵∠1=∠2(已知),
且∠1=∠CGD( ),
∴∠2=∠CGD(等量代换).
∴CE∥BF( ).
∴∠ =∠C( ).
又∵∠B=∠C(已知),
∴∠ =∠B(等量代换).
∴AB∥CD( ).
-
科目: 来源: 题型:
查看答案和解析>>【题目】一只不透明的袋子中装有3个球,球上分别标有数字0,1,2,这些球除了数字外其余都相同,甲、以两人玩摸球游戏,规则如下:先由甲随机摸出一个球(不放回),再由乙随机摸出一个球,两人摸出的球所标的数字之和为偶数时则甲胜,和为奇数时则乙胜.
(1)用画树状图或列表的方法列出所有可能的结果;
(2)这样的游戏规则是否公平?请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC中,AB=AC,E在BA的延长线上,AD平分∠CAE.
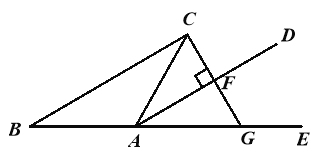
(1)求证:AD∥BC;
(2)过点C作CG⊥AD于点F,交AE于点G.若AF=4,求BC的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法中,正确的个数是( ) ①斜边和一直角边对应相等的两个直角三角形全等;
②有两边和它们的对应夹角相等的两个直角三角形全等;
③一锐角和斜边对应相等的两个直角三角形全等;
④两个锐角对应相等的两个直角三角形全等.
A.1个
B.2个
C.3个
D.4个 -
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的两边及其夹角,求作这个三角形时,第一步骤应为( )
A. 作一条线段等于已知线段
B. 作一个角等于已知角
C. 作两条线段等于已知三角形的边,并使其夹角等于已知角
D. 先作一条线段等于已知线段或先作一个角等于已知角
相关试题

