【题目】如图,在△ACD中,AD=9,CD=3![]() ,△ABC中,AB=AC.
,△ABC中,AB=AC.
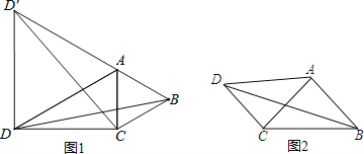
(1)如图1,若∠CAB=60°,∠ADC=30°,在△ACD外作等边△ADD′
①求证:BD=CD′;
②求BD的长.
(2)如图2,若∠CAB=90°,∠ADC=45°,求BD的长.
参考答案:
【答案】(1)①详见解析;②3![]() (2)6
(2)6![]()
【解析】
(1)①根据等边三角形的性质,可得![]() ,
,![]() ,
,![]() 由此可判定△BAD≌△CAD′,根据全等三角形对应边相等即可得出结论;②先证明∠CDD'=90°,在Rt CDD'中根据勾股定理即可求得BD;
由此可判定△BAD≌△CAD′,根据全等三角形对应边相等即可得出结论;②先证明∠CDD'=90°,在Rt CDD'中根据勾股定理即可求得BD;
(2)作AE⊥AD,使AE=AD,连接DE、CE,证明△BAD≌△CAE,即可得BD=CE,然后证明∠CDE=90°,根据勾股定理即可求得CE,由此可得BD.
(1)①证明:∵AB=AC,∠CAB=60°,
∴△ABC是等边三角形,
∴AC=AB=BC,
∵△ADD'是等边三角形,
∴AD=AD'=DD'=9,∠ADD'=∠DAD'=60°,
∴∠BAD=∠CAD',
在△BAD和△CAD′中, ,
,
∴△BAD≌△CAD′(SAS),
∴BD=CD';
②解:∵∠ADD'=60°,∠ADC=30°,
∴∠CDD'=90°,
∴CD'=![]() =
=![]() =3
=3![]() ,
,
∴BD=3![]() ;
;
(2)解:作AE⊥AD,使AE=AD,连接DE、CE,如图2所示:

则△ADE是等腰直角三角形,
∴∠ADE=45°,DE=![]() AD=9
AD=9![]() ,
,
∴∠BAC+∠DAC=∠DAE+∠DAC,
即∠BAD=∠CAE,
在△BAD和△CAE中,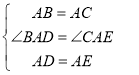 ,
,
∴△BAD≌△CAE(SAS),
∴BD=CE,
∵∠ADE=45°,∠ADC=45°,
∴∠CDE=90°,
∴CE=![]() =
=![]() =6
=6![]() ,
,
∴BD=6![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】问题探究:
如图1,△ACB和△DCE均为等边三角形,点A、D、E在同一直线上,连接BE.
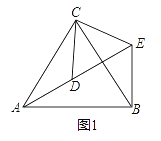
(1)证明:AD=BE;
(2)求∠AEB的度数.
问题变式:
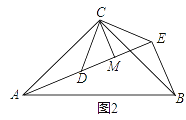
(3)如图2,△ACB和△DCE均为等腰直角三角形,∠ACB=∠DCE=90°,点A、D、E在同一直线上,CM为△DCE中DE边上的高,连接BE.(Ⅰ)请求出∠AEB的度数;(Ⅱ)判断线段CM、AE、BE之间的数量关系,并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形
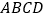 的边长为
的边长为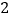 ,点
,点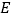 、
、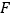 分别为边
分别为边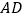 、
、 上的点,
上的点,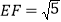 ,点
,点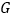 、
、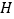 分别为
分别为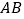 、
、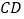 边上的点,连接
边上的点,连接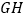 ,若线段
,若线段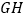 与
与 的夹角为
的夹角为 ,则
,则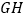 的长为( )
的长为( )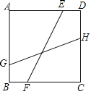
A.
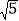 B.
B. 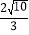 C.
C. 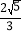 D.
D. 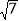
-
科目: 来源: 题型:
查看答案和解析>>【题目】二次函数y=ax2+bx+c(a≠0)的部分图象如图,图象过点(﹣1,0),对称轴为直线x=2,下列结论:
①4a+b=0;②9a+c>3b;③8a+7b+2c>0;④当x>﹣1时,y的值随x值的增大而增大;⑤当函数值y<0时,自变量x的取值范围是x<-1或x>5.
其中正确的结论有( )

A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA=OB,△OAB的面积是2.
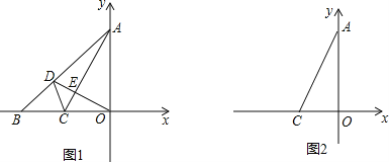
(1)求线段OB的中点C的坐标.
(2)连结AC,过点O作OE⊥AC于E,交AB于点D.
①直接写出点E的坐标.
②连结CD,求证:∠ECO=∠DCB;
(3)点P为x轴上一动点,点Q为平面内一点,以点A.C.P.Q为顶点作菱形,直接写出点Q的坐标.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某地区遭受严重的自然灾害,空军某部队奉命赶灾区空投物资,已知空投物资离开飞机后在空中沿抛物线降落,抛物线顶点为机舱航口
 ,如图所示,如果空投物资离开
,如图所示,如果空投物资离开 处后下落的垂直高度
处后下落的垂直高度 米时,它测
米时,它测 处的水平距离
处的水平距离 米,那么要使飞机在垂直高度
米,那么要使飞机在垂直高度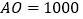 米的高空进行空投,物资恰好准确地落在居民点
米的高空进行空投,物资恰好准确地落在居民点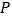 处,飞机到
处,飞机到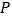 处的水平距离
处的水平距离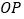 应为________米.
应为________米.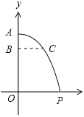
-
科目: 来源: 题型:
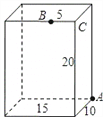
查看答案和解析>>【题目】如图,长方体的长为15厘米,宽为10厘米,高为20厘米,点B到点C的距离是5厘米。一只小虫在长方体表面从A爬到B的最短路程是__________
相关试题

